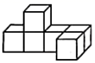
 C .
C .  D .
D . 
甲 | 乙 | 丙 | 丁 | |
平均数 | 9.6 | 9.5 | 9.5 | 9.6 |
方差 | 0.28 | 0.27 | 0.25 | 0.25 |
若从这四人中,选出一位成绩较好且状态稳定的选手参加比赛,那么应选( )


b.甲滑雪场游客消费额的数据在这一组的是:
410 430 430 440 440 440 450 450 520 540
c.甲、乙两个滑雪场游客消费额的数据的平均数、中位数如下:
平均数 | 中位数 | |
甲滑雪场 | 420 | m |
乙滑雪场 | 390 | n |
根据以上信息,回答下列问题:


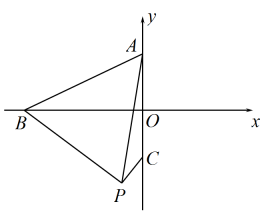
①求满足条件的所有点H的坐标
②当点H在线段上时,点Q是平面直角坐标系内一点,保持
, 连接
, 将线段
绕着点Q顺时针旋转90°,得到线段
, 连接
, 请直接写出线段
的取值范围.