
已知:如图,钝角 . 求作:射线
, 使
.
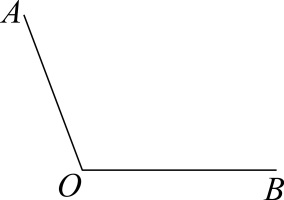
作法:
①在射线上任取一点
;
②以点为圆心,
长为半径作弧,交
于点
;
③分别以点为圆心,大于
长为半径作弧,在
内,两弧相交于点
;
④作射线 . 则
为所求作的射线.
证明:连接CD,CE,
由作图步骤②可知OD= ▲ ,
由作图步费③可知CD= ▲ ,
∵OC=OC,
∴△OCD≅△OCE.
∴∠AOC=∠BOC( )(填推理的依据).
七年级:74 97 96 72 98 99 72 73 76 74 74 69 76 89 78 74 99 97 98 99
八年级:76 88 93 89 78 94 89 94 95 50 89 68 65 88 77 87 89 88 92 91
整理数据如下
|
成绩 人数 年级 |
50≤x≤59 |
60≤x≤69 |
70≤x≤79 |
80≤x≤89 |
90≤x≤100 |
|
七年级 |
0 |
1 |
10 |
1 |
a |
|
八年级 |
1 |
2 |
3 |
8 |
6 |
分析数据如下
|
年级 |
平均数 |
中位数 |
众数 |
方差 |
|
七年级 |
84.2 |
77 |
74 |
138.56 |
|
八年级 |
84 |
b |
89 |
129.7 |
根据以上信息,回答下列问题