
准备在“①国产片,②科幻片,③动作片,④喜剧片,⑤亿元大片”中选取三个作为该问题的备选答案,选取合理的是( )
①总体是指这批日光灯管的全体;②个体是指每只日光灯管的使用寿命;③样本是指从中抽取的30只日光灯管的使用寿命;④样本容量是30只.
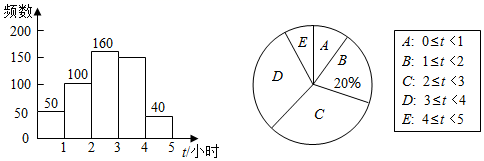
根据图中信息,解答下列问题:

①调查的样本容量是1200;
②个体是每个学生的知识测试等级
③条形统计图中“D”等级的人数超过“A”等级的人数的一半;
④扇形统计图主要用于表示总体中各部分所占的百分比.
分组 | 频数 |
A:60~70 | 4 |
B:70~80 | 12 |
C:80~90 | 16 |
D:90~100 | △ |
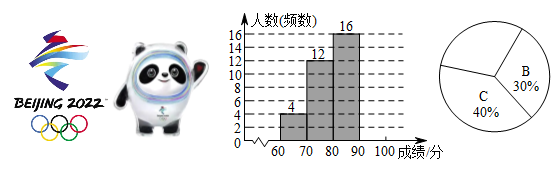
|
成绩x/分 |
频数 |
频率 |
|
50≤x<60 |
10 |
0.10 |
|
60≤x<70 |
25 |
0.25 |
|
70≤x<80 |
30 |
b |
|
80≤x<90 |
a |
0.20 |
|
90≤x≤100 |
15 |
0.15 |
请根据所给信息,解答下列问题:
