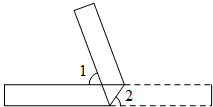
 B .
B .  C .
C .  D .
D . 

⑴将向右平移6个单位长度,再向下平移5个单位长度,画出
平移后的图形为
;
⑵画出绕A点顺时针方向旋转
后的图形为
.
甲 | 乙 | |
进价/(元/本) | ||
售价/(元/本) | 20 | 13 |

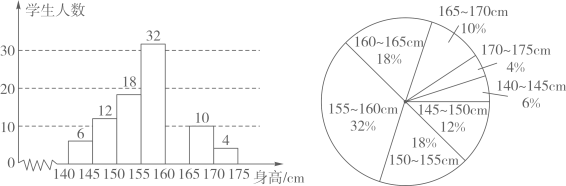
①七年级身高在的学生有 ▲ 人;
②七年级样本的中位数所在范围是 ▲ , 请说明理由;
|
年级 |
七 |
八 |
九 |
|
|
157 |
160 |
169 |
|
|
0.8 |
0.6 |
0.9 |
那么学生的身高比较整齐是哪个年级?为什么.