一、选择题(本大题共10个小题,每小题3分,共30分)
-
-
-
-
-
5.
(2023八下·岳池期中)
已知a、b、c是三角形的三边长,若满足(a-6)
2+

+|c-10|=0,则这个三角形的形状是( )
A . 等腰三角形
B . 等边三角形
C . 直角三角形
D . 等腰直角三角形
-
A . 12
B . 144
C . 13
D . 194
-
A . 40°
B . 45°
C . 50°
D . 60°
-
A . 11
B . 12
C . 16
D . 22
-
-
10.
(2023八下·岳池期中)
如图,在边长为6的正方形ABCD中,点M为对角线BD上一动点,ME⊥BC于E,MF⊥CD于F,则EF的最小值为( )

A . 3
B . 2
C .  D .
D . 
二、填空题(本大题共6个小题,每小题3分,共18分)
-
-
-
13.
(2023八下·岳池期中)
如图,为了测量池塘边A、B两地之间的距离,在线段AB的同侧取一点C,连结CA并延长至点D,连结CB并延长至点E,使得A、B分别是CD、CE的中点,若DE=18m,则线段AB的长度是
m.

-
-
15.
(2023八下·岳池期中)
如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为25,DE=2,则AE的长为
-
16.
(2023八下·岳池期中)
如图,四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此进行下去……记正方形ABCD的边长为a
1=1,按上述方法所作的正方形的边长依次为a
2、a
3、a
4……、a
n , 则a
n=
(用含n的式子表示) .

三、解答下列各题(本大题共4个小题,每小题各6分,共24分)
-
-
-
19.
(2023八下·岳池期中)
已知:如图,在

ABCD中,E、F为AC上的两点,且AE=CF,连接BE、DF,求证:BE=DF.

-
20.
(2023八下·岳池期中)
如图,在

ABCD中,AE⊥BC于点E,延长BC至点F,使CF=BE,连接DF,求证:四边形AEFD是矩形.

四、实践应用(本大题共3个小题,第21、22题各8分,第23题6分,共22分)
-
21.
(2023八下·岳池期中)
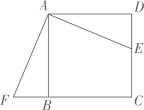
岳池中学校园建设中,有一块四边形的空地ABCD.如下图所示,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,AD=4m,BC=12m,CD=13m,若每平方米草皮需要200元,问学校需要投入多少资金买草皮?

-
22.
(2023八下·岳池期中)
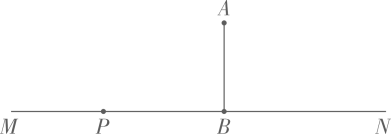
为了把“广安民用运输机场选址岳池普安”宣传到各村,普安镇政府采用了移动宣讲的形式进行宣传动员如图,笔直公路MN的一侧点A处有一村庄,村庄A到公路MN的距离为800米,假使宣讲车P周围1000米以内能听到广播宣传,宣讲车P在公路MN上沿PN方向行驶时:
-
-
(2)
如果能听到,已知宣讲车的速度是每分钟300米,那么村庄总共能听到多长时间的宣传?
-
23.
(2023八下·岳池期中)
如图,正方形网格中每个小正方形的边长都是1,每个小正方形的顶点叫做格点,现以点A、B、C、D、E这5个格点中的3点为顶点画三角形.

-
(1)
在图①中画一个等腰三角形,要求顶角不是直角;
-
(2)
在图②中画一个直角三角形,要求两直角边不相等;
-
五、推理论证(本大题共2个小题,每小题各8分,共16分)
-
24.
(2023八下·岳池期中)
如图,已知AC是矩形ABCD的对角线,AC的垂直平分线EF分别交BC、AD于点E和F,EF交AC于点O.

-
-
(2)
若AB=6,AD=8,求四边形AECF的周长.
-
25.
(2023八下·岳池期中)
如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC于F,交直线MN于E,连接CD、BE.

-
-
(2)
当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由.
六、拓展探究(共10分)
-
26.
(2023八下·岳池期中)
如图,在

ABCD中,AD=9cm,AB=3

cm,∠B=45°,点M、N分别以A、C为起点,1cm/秒的速度沿AD、CB边运动,设点M、N运动的时间为t秒(0≤t≤6)

-
-
(2)
连接AN、CM,当t为何值时,四边形AMCN为菱形;
-
(3)
作MP⊥BC于P,NQ⊥AD于Q,当t为何值时,四边形MPNQ为正方形.











