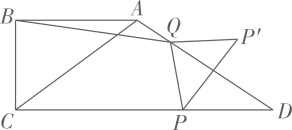
B .
B .  C .
C .  D .
D . 


竞赛成绩统计表
组别 | 分数 | 人数 |
A组 | 4 | |
B组 | ||
C组 | 10 | |
D组 | ||
E组 | 14 |
竞赛成绩扇形统计图

参考数据:sin22°≈ , cos22°≈
, tan22°≈
, sin67°≈
, cos67°≈
, tan67°≈
.
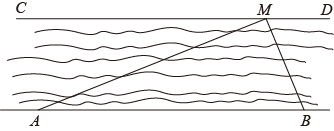
如图1,和
都是等边三角形,连接
. 求证:
.

如图2,和
都是等腰直角三角形,
. 连接
. 请直接写出
的值.
如图3,和
都是直角三角形,
, 且
. 连接
. 延长
交
于点F,交
于点G.求
的值.
x | 40 | 70 | 90 |
y | 180 | 90 | 30 |