
 B .
B .  C .
C .  D .
D . 
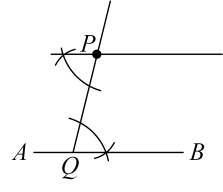 B .
B .  C .
C . 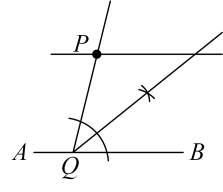 D .
D . 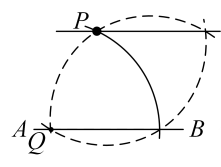

小禾的解法:
| 小禾的检验:当 ∵ ∴分解因式错误. |
任务:
项目 | 应聘者 | ||
甲 | 乙 | 丙 | |
学历 | 9 | 8 | 8 |
经验 | 8 | 6 | 9 |
能力 | 7 | 8 | 8 |
态度 | 5 | 7 | 5 |
①求y关于x的函数表达式.
②若竖立的方盒的高为 , 求x的最大值.
①求杯子与水平线的夹角
的度数.
②由图2到图3,点A的位置是升高了还是下降了?变化了多少厘米?(结果精确到 , 参考数据:
)