
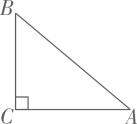

 B .
B . 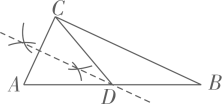 C .
C .  D .
D . 





a.七年级m名学生一周内发言次数的频数分布直方图如下:
(数据分成6组:0≤x<4,4≤x<8,8≤x<12,12≤x<16,16≤x<20,20≤x<24) .
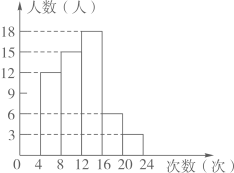
b.七年级m名学生一周内发言次数在8≤x<12这一组的是:
8 9 9 9 9 10 10 10 10 10 10 10 11 11 11
c.一周内发言次数的平均数、中位数、众数如下:
问题 | 平均数(单位:次) | 中位数(单位:次) | 众数(单位:次) |
七年级 | 12 | n | 10 |
八年级 | 11 | 10 | 9 |
九年级 | 10 | 10 | 9 |
根据以上信息,回答下列问题,

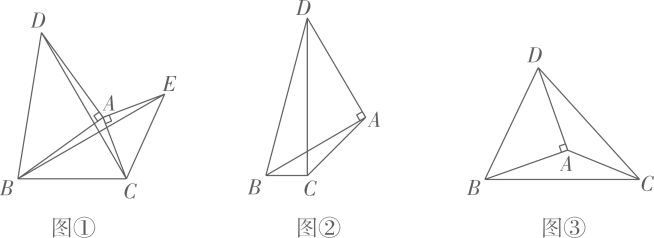
[感知]如图①,以△ABC的边AB、AC为直角边,A为直角顶点,向外作等腰直角△ABD和等腰直角△ACE,连结BE、CD,易知△ADC≌△ABE.(不要求证明)
[探究]如图②,在△ABC中,已知∠ACB=135°,∠BAD=90°,BC=1,AC=2,AB=AD,求CD的长.
[应用]如图③,在△ABC中,BC=2,AC=1.以△ABC的边AB为直角边,A为直角顶点,向外作等腰直角△ABD,则线段CD长度的最大值是 ▲
