广东省深圳市龙华区2022-2023学年下学期九年级调研测试...

更新时间：2024-07-13 浏览次数：107 类型：月考试卷

一、选择题(本大题共10小题，每小题3分，共30分。)

1. (2023九下·深圳月考) 砚台与笔、墨、纸是中国传统的文房四宝，是中国书法的必备用具．下图是一方寓意“规矩方圆”的砚台，它的俯视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2024七下·启东期末) 在《九章算术》一书中，对开方开不尽的数起了一个名字，叫做“面”．这是中国传统数学对无理数的最早记载．下面符合“面”的描述的数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023九下·深圳月考) 下列运算正确的是（）

A . x²+x²=x⁴ B . y³·y²=y⁶ C . (x+y)(x-y)=x²-y² D . (x+y)²=x²+y²

答案解析收藏纠错 + 选题
4. (2023九下·深圳月考) 农户利用“立体大棚种植技术”把毛豆和芹菜进行混种．已知毛豆齐苗后棚温在18~25℃最适宜，播种芹菜的最适宜温度是15~20℃．农户在毛豆齐苗后在同一大棚播种了芹菜，这时应该把大棚温度设置在下列哪个范围最适宜（）

A . 15~18℃ B . 18~20℃ C . 20~25℃ D . 20℃以上

答案解析收藏纠错 + 选题
5. (2023·深圳模拟) 如图，某商场有一自动扶梯，其倾斜角为α，高为h米，扶梯的长度是（）

A . $\text{[math]}$ B . hcosα C . hsinα D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023九下·深圳月考) 下图是小杰同学家中的一个30min沙漏计时器，相关实验结果表明，沙漏中的沙下落的速度可以近似看成匀速，从计时器开始计时到计时30min止，上面玻璃球内的含沙量Q(cm³)与时间t(min)之间的函数关系图象大致为（）

A . B . C . D .

答案解析收藏纠错 + 选题
7. (2023九下·深圳月考) 如图，这条活灵活现的“小鱼”是由若干条线段组成的，它是一个轴对称图形，对称轴为直线I，则下列结论不一定正确的是（）

A . 点C和点D到直线I的距离相等 B . BC=BD C . ∠CAB=∠DAB D . 四边形ADBC是菱形

答案解析收藏纠错 + 选题
8. (2023·深圳模拟) 如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，D，E分别是BC，AC的中点，连接DE．以点A为圆心，适当长度为半径作弧，分别交AC，AB于点M，N；以点D为圆心，AM长为半径作弧交DE于点P；以点P为圆心，MN长为半径作弧，交前面的弧于点Q；作射线DQ交AB于点F．则AF的长为（）

A . 3 B . 4 C . 5 D . 6

答案解析收藏纠错 + 选题
9. (2024九下·云南模拟) 某公司去年10月份的营业额为2500万元，后来公司改变营销策略，12月份的营业额达到3780万元，已知12月份的增长率是11月份的1.3倍，求11月份的增长率。设11月份的增长率为x，根据题意，可列方程为（）

A . 2500(1+x)(1+1.3x)=3780 B . 2500(1+x)²=3780 C . 2500(1+1.3x)²=3780 D . 2500(1+2.3x)=3780

答案解析收藏纠错 + 选题
10. (2023·深圳模拟) 如图，在Rt△ABC中，∠ACB=90°，D是AB上一点，连接CD，若∠ACD=2∠B， $\text{[math]}$ ，则 $\text{[math]}$ 的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题(本大题共5小题，每小题3分，共15分)

11. (2023九下·深圳月考) 计算：|-5|+tan45°=

答案解析收藏纠错 + 选题
12. (2023九下·深圳月考) 新学期开始，小颖从学校开设的感兴趣的5门劳动教育课程：烹饪、茶艺、花卉种植、整理收纳、家电维修中，随机选择-一门课程学习，她选择“茶艺”课程的概率是．

答案解析收藏纠错 + 选题
13. (2023·深圳模拟) 已知 $\text{[math]}$ 是方程组 $\text{[math]}$ 的解，则m+n=．

答案解析收藏纠错 + 选题
14. (2023九下·深圳月考) 如图，在平面直角坐标系中，OA=3，将OA沿y轴向上平移3个单位至CB，连接AB，若反比例函数y= $\text{[math]}$ (x>0)的图象恰好过点A与BC的中点D，则k=．

答案解析收藏纠错 + 选题
15. (2023·深圳模拟) 如图，在边长为4米的正方形场地ABCD内，有一块以BC为直径的半圆形红外线接收“感应区”，边AB上的P处有一个红外线发射器，红外线从点P发射后，经AD、CD．上某处的平面镜反射后到达“感应区”．若AP=1米，当红外线途经的路线最短时，AD上平面镜的反射点距离点A米．

答案解析收藏纠错 + 选题

三、解答题(本大题共7小题，共55分)

16. (2023·深圳模拟) 解不等式组 $\text{[math]}$

答案解析收藏纠错 + 选题
17. (2024九下·福田模拟) 先化简、再求值： $\text{[math]}$ ，其中x=2．

答案解析收藏纠错 + 选题
18. (2023九下·深圳月考) 为了解九年级学生对某个知识点的掌握程度，某校对九年级学生以20人一组进行了随机分组，开展了一次素养调研，并用SOLO评分模型进行评分：“完全不理解”记为0分，“了解了一个方面”记为1分，“了解了几个独立的方面”记为2分，“理解了几个方面的相关性”记为3分，“能够综合运用”记为4分，现从调查结果中随机抽取了3个小组学生的得分，进行统计分析，过程如下：
[整理与描述]
1. （1）请补全第1小组得分条形统计图：第2小组得分扇形统计图中，“得分为3 分”这一项所对应的圆心角的度数为°
2. （2） [分析与估计]
  
  平均数
  众数
  中位数
  第1组
  2.9
  a
  3
  第2组
  b
  0
  1
  第3组
  2.25
  2
  c
  由上表填空：a=，b=，c=；
3. （3）若该校九年级有600名学生，请你估计该校九年级学生在调研中表现为“能够综合运用”的人数有人；
4. （4） [评价与建议]
  结合你的分析，请给第2组的同学提供一条有关该知识点的学习建议．
答案解析收藏纠错 + 选题
19. (2023九下·深圳月考) 如图，⊙O是△ABC的外接圆，连接OA，过点C作一条射线CD．
1. （1）请从以下条件中：①CD∥AO，∠ABC=45°；②∠BCD=∠BAC；③CB平分∠ACD．选择一组能证明CD是⊙O的切线的条件，并写出证明过程；
2. （2）若OA=2，∠OAB=22.5°，AB=CB，求 $\text{[math]}$ 的长度．(结果保留π)
答案解析收藏纠错 + 选题
20. (2023九下·深圳月考) 随着天气转暖，越来越多的市民喜欢到户外活动，小明与同学约定周末带帐篷到附近露营地开展活动．
1. （1） [买帐篷]经了解，某种帐篷有A、B两种型号，已知A型帐篷的单价比B型帐篷的单价多30元，用1200元购买A型帐篷的数量和用900元购买B型帐篷的数量相同．小明买了A、B两种型号帐篷各2个，共需多少钱？
2. （2） [摆帐篷]周末，小明与同学一起来到露营地，发现有一块由篱笆围绕的长20米，宽14米的矩形草地(抽象成如图11的20×14的方格纸)可用来摆帐篷．经测量，每个帐篷占据的地面部分是半径为3米的圆形(抽象成如图10的圆)，为保障通行，帐篷四周需要留有通道，通道最狭窄处的宽度不小于I米．小明将第一个帐篷按要求摆放在如图所示的位置，此块草地内最多还能摆下几个同样大小的帐篷呢？请在图11中画出符合要求的设计示意图．(要求：圆心要画在格点上，画圆时要用圆规)
答案解析收藏纠错 + 选题
21. (2023九下·深圳月考) 如图：
1. （1） [课本再现]把两个全等的矩形ABCD和矩形CEFG拼成如图12的图案，则∠ACF= °
2. （2） [迁移应用]如图13，在正方形ABCD中，E是CD边上一点(不与点C，D重合)，连接BE，将BE绕点E顺时针旋转90°至FE，作射线FD交BC的延长线于点G，求证：CG=BC；
3. （3） [拓展延伸]在菱形ABCD中，∠A=120°，E是CD边上一点(不与点C，D重合)，连接BE，将BE绕点E顺时针旋转120°至FE，作射线FD交BC的延长线于点G．
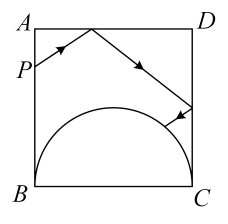
  ①线段CG与BC的数量关系是；
  ②若AB=6，E是CD的三等分点，则△CEG的面积为。
答案解析收藏纠错 + 选题
22. (2023九下·深圳月考) [定义]若抛物线与一水平直线交于两点，我们把这两点间线段的长称为抛物线关于这条直线的跨径，抛物线的顶点到该直线的距离称为抛物线关于这条直线的矢高，矢高与跨径的比值称为抛物线关于这条直线的矢跨比．
1. （1）如图，抛物线y=ax²+bx+c的顶点为P，PC⊥x轴于点C，它与x轴交于点A，B，则AB的长为抛物线y=ax²+bx+c关于x轴的跨径，PC的长为抛物线y=a²+bx+c关于x轴的矢高， $\text{[math]}$ 的值为抛物线y=ax²+bx+c关于x轴的矢跨比．
2. （2） [特例]如图15，已知抛物线y=-x²+4与x轴交于点C，D (点C在点D右侧)：
  ①抛物线y=-x²+4关于x轴的矢高是，跨径是，矢跨比是；
  ②有一抛物线经过点c，与抛物线y=-x²+4开口方向与大小一样，且矢高是抛物线y=-x²+4关于x轴的矢高的 $\text{[math]}$ ，求它关于x轴的矢跨比；
3. （3） [推广]结合抛物线的平移规律可以发现，两条开口方向与大小一样的抛物线，若第一条抛物线的矢高是第二条抛物线关于同一直线的矢高的k(k>0)倍，则第一条抛物线的跨径是第二条抛物线关于同一直线的跨径的倍(用含k的代数式表示)；
4. （4） [应用]如图16是某地一座三拱桥梁建筑示意图，其中主跨与边跨的拱轴线为开口方向与大小一样的抛物线，它们关于水平钢梁所在直线的跨径分别为420米与280米，已知主跨的矢跨比为 $\text{[math]}$ ，则边跨的矢跨比是。
答案解析收藏纠错 + 选题