 B .
B .  C .
C .  D .
D . 

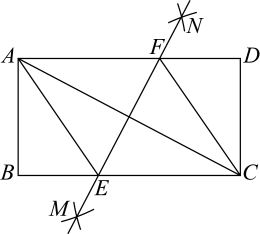
①四边形是菱形;②
;③
;④若
平分
, 则
.
其中正确结论的个数是( )
①;②
;③
;④若
和
均在该函数的图象上,且
, 则
.
其中正确的结论有.(填序号)

学生每周自主发展兴趣爱好时长频数分布表
|
组别 |
时长t(单位: |
人数累计 |
人数 |
|
A |
|
正正正正正正正正 |
40 |
|
B |
|
正正正正正正正正正正 |
50 |
|
C |
|
正正正正正正正正正正正正正正正正 |
80 |
|
D |
|
正正正正正正 |
30 |
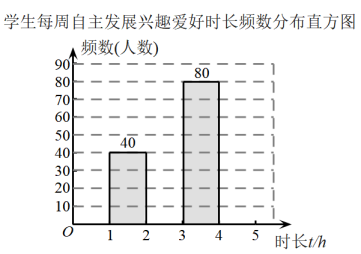
根据以上信息,解答下列问题:
