题库组卷系统-专注K12在线组卷服务

在线咨询

当前：初中数学

当前位置：初中数学 /中考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

吉林省吉林市船营区2023年中考一模数学试卷

更新时间：2023-07-05 浏览次数：55 类型：中考模拟

一、单选题

1. (2023·船营模拟) 中国是最早采用正负数表示相反意义的量并进行负数运算的国家.若气温上升 $\text{[math]}$ ，记作： $\text{[math]}$ ，那么气温下降 $\text{[math]}$ 可记作（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023·船营模拟) 《九章算术》中将底面是直角三角形的直三棱柱称之为“堑堵”，如图所示.按图放置的“堑堵”，它的俯视图为（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2024九下·长春模拟) 已知 $\text{[math]}$ ，则一定有 $\text{[math]}$ ， “ $\text{[math]}$ ”中应填的符号是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的平分线 $\text{[math]}$ 交 $\text{[math]}$ 边于点E ，则 $\text{[math]}$ 的长是（）

A . 5 B . 7 C . 3.5 D . 3

答案解析收藏纠错 + 选题
5. (2023八下·徐汇期末) 一次函数 $\text{[math]}$ 的图象不经过的象限是（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
6. (2023·船营模拟) 如图， $\text{[math]}$ 是 $\text{[math]}$ 的直径， $\text{[math]}$ 为 $\text{[math]}$ 上一点，过点 $\text{[math]}$ 的切线与 $\text{[math]}$ 的延长线交于点 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

7. (2023八上·银川期末) 如果二次根式 $\text{[math]}$ 有意义，那么实数a的取值范围是．

答案解析收藏纠错 + 选题
8. (2023七下·南京期末) a与3的和是正数，用不等式表示为.

答案解析收藏纠错 + 选题
9. (2024九下·上海市模拟) 计算：（3a³）²= ．

答案解析收藏纠错 + 选题
10. (2023·船营模拟) 已知二元一次方程组 $\text{[math]}$ 则 $\text{[math]}$ 的值为.

答案解析收藏纠错 + 选题
11. (2023·船营模拟) 将一副三角板按如图所示的方式摆放，点A在 $\text{[math]}$ 边上， $\text{[math]}$ ，则 $\text{[math]}$ 的度数是°.

答案解析收藏纠错 + 选题
12. (2023·船营模拟) 如图，在平面直角坐标系中，点 $\text{[math]}$ 的坐标 $\text{[math]}$ ，点 $\text{[math]}$ 坐标 $\text{[math]}$ ，连接 $\text{[math]}$ 将线段 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ 后，点 $\text{[math]}$ 的坐标变为.

答案解析收藏纠错 + 选题
13. (2023·船营模拟) 如图，已知 $\text{[math]}$ 是小正方形的外接圆，是大正方形的内切圆.若大正方形的边长是2，则图中阴影部分的面积为．

答案解析收藏纠错 + 选题
14. (2023·船营模拟) 点 $\text{[math]}$ 在抛物线 $\text{[math]}$ 上，且点P到y轴的距离小于1，则n的取值范围是.

答案解析收藏纠错 + 选题

三、解答题

15. (2023·船营模拟) 下面解题过程中，第一步就出现了错误，但最后所求得的值是正确的.
1. （1）请写出正确的化简过程；
2. （2）图中被遮住的x的值是.
答案解析收藏纠错 + 选题
16. (2023·船营模拟) 如图，在平行四边形 $\text{[math]}$ 中，E ， F分别是 $\text{[math]}$ ， $\text{[math]}$ 的中点，点G ， H分别在 $\text{[math]}$ ， $\text{[math]}$ 上，且 $\text{[math]}$ ．求证： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
17. (2023·船营模拟) 一个不透明的袋子中装有1个白球，1个黄球，2个红球，这些球除颜色外都相同.搅匀后从中任意摸出1个球，记下颜色后放回，搅匀，再从中任意摸出1个球，请用画树状图法或列表法求两次摸到的球都是红球的概率.

答案解析收藏纠错 + 选题
18. (2023·船营模拟) 今年的3月12日是我国第45个植树节.某学校为美化校园需补栽甲、乙两种树苗.咨询商家得知，甲种树苗每株比乙种树苗便宜10元，最后分别用600元，800元购买了相同数量的两种树苗.求甲种树苗的单价.

答案解析收藏纠错 + 选题
19. (2023·前郭模拟) 如图，在 $\text{[math]}$ 的方格纸中，已知格点P ，请按要求画格点图形（顶点均在格点上）．
1. （1）在图1中画一个锐角三角形，使P为其中一边的中点，再画出该三角形向右平移2个单位后的图形．
2. （2）在图2中画一个以P为一个顶点的钝角三角形，使三边长都不相等，再画出该三角形绕点P旋转 $\text{[math]}$ 后的图形．
答案解析收藏纠错 + 选题
20. (2023·船营模拟) 已知蓄电池的电压U为定值，使用蓄电池时，电流I（单位：A）与电阻R（单位：Ω）是反比例函数关系，它的图象如图所示．
1. （1）求这个反比例函数的表达式；
2. （2）如果以此蓄电池为电源的用电器的限制电流不能超过10A ，那么用电器的可变电阻R应控制在什么范围？请根据图象，直接写出结果．
答案解析收藏纠错 + 选题
21. (2023·船营模拟) 林林将一张纸对折后做成了纸飞机如图①所示，纸飞机机尾的横截面是一个轴对称图形，其示意图如图②所示，已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．连结 $\text{[math]}$ ，求线段 $\text{[math]}$ 的长．（结果精确到 $\text{[math]}$ ．）(参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ． )

答案解析收藏纠错 + 选题
22. (2023·船营模拟) 为了了解甲、乙、丙三种型号的扫地机器人的扫地质量，工作人员从某月生产的甲、乙、丙三种型号扫地机器人中各随机抽取10台，在完全相同条件下试验，记录下它们的除尘指数的数据，并进行整理、描述和分析，下面给出了部分信息．
ⅰ.甲、乙两种型号扫地机器人除尘指数的折线图：

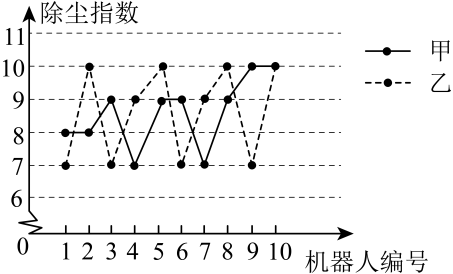
ⅱ.丙型号扫地机器人的除尘指数数据：10，10，10，9，9，8，3，9，8，10.

ⅲ．甲、乙、丙三种型号机器人除尘指数的平均数：

扫地机器人

甲

乙

丙

除尘指数平均数

8.6

8.6

m

根据以上信息，回答下列问题：
1. （1）求表中m的值；
2. （2）在抽取的扫地机器人中，如果除尘指数的10个数据的方差越小，则认为该型号的扫地机器人性能更稳定．据此推断：在甲、乙两种型号扫地机器人中，型扫地机器人的性能稳定（填“甲”或“乙”）；
3. （3）在抽取的扫地机器人中，如果把10个除尘指数去掉一个最高值和一个最低值之后的平均值作为性能参考，平均值越高，则认为该型号扫地机器人性能表现越优秀．据此推断：在甲、乙、丙三种型号的扫地机器人中，表现最优秀的是（填“甲”、“乙”或“丙”）．
答案解析收藏纠错 + 选题
23. (2023·船营模拟) 甲、乙两家快递站分别接到了对自己所辖范围派送快递各 $\text{[math]}$ 件的任务，甲快递站前期先派送了 $\text{[math]}$ 件后，甲、乙两家快递站同时以相同的速度派送，甲快递站经过a小时后总共派送 $\text{[math]}$ 件，由于人员变化，派送速度变慢，结果 $\text{[math]}$ 小时完成派送任务，乙快递站8小时完成派送任务，在某段时间内，甲、乙两家快递站的派送件数y(件)与派送时间x(小时)之间的关系如图所示：
1. （1）乙快递站每小时派送件，a的值为；
2. （2）甲快递站派送速度变慢后，求y关于x的函数解析式，并写出自变量x的取值范围；
3. （3）当乙快递站完成派送任务时，求甲快递站未派送的快递件数．
答案解析收藏纠错 + 选题
24. (2023·船营模拟) 【问题】如图①， $\text{[math]}$ 和 $\text{[math]}$ 都是等腰直角三角形， $\text{[math]}$ ，点D在 $\text{[math]}$ 上．求证： $\text{[math]}$ ．
1. （1）【感知】连接 $\text{[math]}$ ，则 $\text{[math]}$ ， $\text{[math]}$ ．从而得出 $\text{[math]}$ 为直角三角形，使问题得证．请你根据以上思路，写出完整证明过程．
2. （2）【应用】如图②，四边形 $\text{[math]}$ 和四边形 $\text{[math]}$ 都是正方形，点D在对角线 $\text{[math]}$ 上．若 $\text{[math]}$ ， $\text{[math]}$ ，正方形 $\text{[math]}$ 的面积是．
3. （3）【拓展】如图③， $\text{[math]}$ 和 $\text{[math]}$ 都是等边三角形，点A在 $\text{[math]}$ 上，连接 $\text{[math]}$ ．若 $\text{[math]}$ ， $\text{[math]}$ ，请直接写出 $\text{[math]}$ 的面积．
答案解析收藏纠错 + 选题
25. (2023·船营模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，动点P从点B出发，以 $\text{[math]}$ 的速度沿线段 $\text{[math]}$ 向终点A运动，当点P不与点B重合时，将线段 $\text{[math]}$ 绕点P旋转得到线段 $\text{[math]}$ ，使 $\text{[math]}$ ，点M始终在 $\text{[math]}$ 的下方，过点M作 $\text{[math]}$ 于点N ，设点P的运动时间为 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 重叠部分的图形面积为 $\text{[math]}$ ．
1. （1）当点M落在线段 $\text{[math]}$ 上时，x的值为；
2. （2）求y关于x的函数关系式，并写出自变量x的取值范围；
3. （3）直接写出在整个运动过程中，点M运动的路程．
答案解析收藏纠错 + 选题
26. (2023·船营模拟) 如图，在平面直角坐标系中，点A的坐标为 $\text{[math]}$ ，取一点 $\text{[math]}$ ，连接 $\text{[math]}$ ，作线段 $\text{[math]}$ 的垂直平分线 $\text{[math]}$ ，过点B作x轴的垂线 $\text{[math]}$ ，记 $\text{[math]}$ ， $\text{[math]}$ 的交点为P.
1. （1）当 $\text{[math]}$ 时，在图中补全图形(尺规作图，不写作法，保留作图痕迹)；
2. （2）小明多次取不同数值b ，得出相应的点P ，并把这些点用平滑的曲线连接起来，发现这些点P竟然在一条曲线L上.设点P的坐标为 $\text{[math]}$ ，试求y与x之间的关系式；
3. （3） ①设点P到x轴，y轴的距离分别为 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的范围是；当 $\text{[math]}$ 时，点P的坐标为；
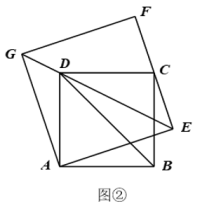
  ②将曲线L在直线 $\text{[math]}$ 下方的部分沿直线 $\text{[math]}$ 向上翻折，得到一条“W”形状的新曲线，若直线 $\text{[math]}$ 与这条“W”形状的新曲线有4个交点，则k的取值范围是.
答案解析收藏纠错 + 选题

试卷信息