四川省内江市隆昌市第七中学2023年中考三模数学试卷

更新时间：2024-07-31 浏览次数：36 类型：中考模拟

一、单选题

1. (2023·隆昌模拟) 如果a与2互为相反数，那么a等于（）

A . 2 B . $\text{[math]}$ C . $\text{[math]}$ D . -2

答案解析收藏纠错 + 选题
2. (2023·隆昌模拟) 2020年是不寻常的一年，据世卫组织统计，截止2020年6月28日全球累计已超过1040万人确诊感染了“新冠”病毒，将数据1040万用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023·隆昌模拟) 如图，一个正方块的六个面分别标有A，B，C，D，E，F，从三个不同方向看到的情况，如图所示，则A的对面应该是字母（）

A . B B . C C . E D . F

答案解析收藏纠错 + 选题
4. 若单项式 $\text{[math]}$ 与 $\text{[math]}$ 的和是单项式，则n的值是（）

A . 3 B . 6 C . 8 D . 9

答案解析收藏纠错 + 选题
5. (2023·隆昌模拟) 函数y＝ $\text{[math]}$ 中自变量x的取值范围是（）

A . x≠0 B . x≥2或x≠0 C . x≥2 D . x≤-2且x≠0

答案解析收藏纠错 + 选题
6. (2023·隆昌模拟) 已知非零实数x满足 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . 5 B . 7 C . 9 D . 11

答案解析收藏纠错 + 选题
7. (2023·隆昌模拟) 按下图所示的程序计算：若开始输入的x值为-2，则最后输出的结果是（）

A . 8 B . 64 C . 120 D . 128

答案解析收藏纠错 + 选题
8. (2023·隆昌模拟) 如图所示，某校数学兴趣小组利用标杆BE测量建筑物的高度，已知标杆BE高为1.5m，测得AB＝3m，BC＝7m，则建筑物CD的高是（）m

A . 3.5 B . 4 C . 4.5 D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2023·隆昌模拟) 设 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 是 $\text{[math]}$ 三边，并且关于 $\text{[math]}$ 的方程 $\text{[math]}$ 有两个相等的实数根，判断 $\text{[math]}$ 的形状，正确的结论是（）

A . 等腰三角形 B . 直角三角形 C . 等腰直角三角形 D . 正三角形

答案解析收藏纠错 + 选题
10. (2023·隆昌模拟) 如图，将△ABC绕点A逆时针旋转100°，得到△ADE，若点D在线段BC的延长线上，则∠ADE的大小为（）

A . 60° B . 50° C . 45° D . 40°

答案解析收藏纠错 + 选题
11. (2023·隆昌模拟) 如图，BD是 $\text{[math]}$ 的直径，弦AC交BD于点G．连接OC，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . 98° B . 103° C . 108° D . 113°

答案解析收藏纠错 + 选题
12. (2023·隆昌模拟) 如图，在正方形 $\text{[math]}$ 中，点P是 $\text{[math]}$ 上一动点(不与 $\text{[math]}$ 重合) ，对角线 $\text{[math]}$ 相交于点O，过点P分别作 $\text{[math]}$ 的垂线，分别交 $\text{[math]}$ 于点 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ．下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ ；⑤点O在 $\text{[math]}$ 两点的连线上．其中正确的是（）

A . ①②③④ B . ①②③⑤ C . ①②③④⑤ D . ③④⑤

答案解析收藏纠错 + 选题

二、填空题

13. (2024八下·锦江期末) 分解因式： $\text{[math]}$ =

答案解析收藏纠错 + 选题
14. (2023·隆昌模拟) 如图所示的图形中，若去掉一个 $\text{[math]}$ 的角得到一个五边形，则 $\text{[math]}$ °．

答案解析收藏纠错 + 选题
15. (2023·隆昌模拟) 如图，Rt△A′BC′是由Rt△ABC绕B点顺时针旋转而得，且点A、B、C′在同一条直线上，在Rt△ABC中，若∠C=90°，BC=2，AB=4，则斜边AB旋转到A′B所扫过的扇形面积为．

答案解析收藏纠错 + 选题
16. (2023·隆昌模拟) 已知Rt△ABC中，∠ACB=90°，AC=BC，D为AB的中点，P为CD上一点，PC：PD=1：2，E在AC上、F在AB上，且∠EPF=135°，且若PE=2，则PF=．

答案解析收藏纠错 + 选题

三、解答题

17. (2024九上·剑阁期中) 先化简，再求值： $\text{[math]}$ ，其中x满足x²－2x－2=0.

答案解析收藏纠错 + 选题
18. (2023·隆昌模拟) 如图，在▱ABCD中，对角线AC，BD交于点O，点E，点F在BD上，且 BE＝DF 连接AE并延长，交BC于点G，连接CF并延长，交AD于点H．
1. （1）求证：△AOE≌△COF；
2. （2）若AC平分∠HAG，求证：四边形AGCH是菱形．
答案解析收藏纠错 + 选题
19. (2023·攀枝花模拟) 为推广阳光体育“大课间”活动，我市某中学决定在学生中开设A：实心球，B：立定跳远，C：跳绳，D：跑步四种活动项目．为了了解学生对四种项目的喜欢情况，随机抽取了部分学生进行调查，并将调查结果绘制成如图①②的统计图．请结合图中的信息解答下列问题：
1. （1）在这项调查中，共调查了多少名学生？
2. （2）请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比，并将两个统计图补充完整；
3. （3）若调查到喜欢“跳绳”的5名学生中有3名男生，2名女生．现从这5名学生中任意抽取2名学生．请用画树状图或列表的方法，求出刚好抽到同性别学生的概率．
答案解析收藏纠错 + 选题
20. (2023·隆昌模拟) 第十一届全国少数民族传统体育运动会于2019年9月8日在郑州举行，其中，花炮、押加、民族式摔跤三个项目的比赛在郑州大学主校区进行．如图，钟楼是郑州大学主校区标志性建筑物之一，小刚站在钟楼前C处测得钟楼顶A的仰角为53°，小强站在对面的教学楼三楼上的D处测得钟楼顶A的仰角为45°，两人的水平距离 $\text{[math]}$ 为4m，已知教学楼三楼所在的高度为10m，根据测量数据，计算钟楼 $\text{[math]}$ 的高度（结果精确到1米，参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

答案解析收藏纠错 + 选题
21. (2023·隆昌模拟) 一家蔬菜公司收购到某种绿色蔬菜140吨，准备加工后进行销售，销售后获利的情况如下表所示：

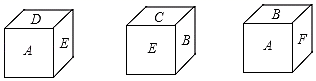
销售方式

粗加工后销售

精加工后销售

每吨获利(元)

1000

2000

已知该公司的加工能力是：每天能精加工5吨或粗加工15吨，但两种加工不能同时进行.受季节等条件的限制，公司必须在一定时间内将这批蔬菜全部加工后销售完.
1. （1）如果要求12天刚好加工完140吨蔬菜，则公司应安排几天精加工，几天粗加工？
2. （2）如果先进行精加工，然后进行粗加工.
  ①试求出销售利润W元与精加工的蔬菜吨数m之间的函数关系式；
  
  ②若要求在不超过10天的时间内，将140吨蔬菜全部加工完后进行销售，则加工这批蔬菜最多获得多少利润？此时如何分配加工时间？
答案解析收藏纠错 + 选题

四、填空题

22. (2024八下·息县月考) 已知xy=3，那么 $\text{[math]}$ 的值为 .

答案解析收藏纠错 + 选题
23. (2023·隆昌模拟) 已知m、n是关于x的一元二次方程x²+px+q＝0的两个不相等的实数根，且m²+mn+n²＝3，则q的取值范围是．

答案解析收藏纠错 + 选题
24. (2023·隆昌模拟) 如图，以△ABC的边AB、AC为边往外作正方形ABEF与正方形ACGD ，连接 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的值为.

答案解析收藏纠错 + 选题
25. (2023·隆昌模拟) 对于实数 $\text{[math]}$ ，规定 $\text{[math]}$ ，例如 $\text{[math]}$ ， $\text{[math]}$ ，那么计算 $\text{[math]}$ 的结果是．

答案解析收藏纠错 + 选题

五、解答题

26. (2024九下·隆昌月考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 点 $\text{[math]}$ 在斜边 $\text{[math]}$ 上，以 $\text{[math]}$ 为直径的 $\text{[math]}$ 与 $\text{[math]}$ 相切于点 $\text{[math]}$
1. （1）求证： $\text{[math]}$ 平分 $\text{[math]}$
2. （2）若 $\text{[math]}$ ①求 $\text{[math]}$ 的值；②求图中阴影部分的面积.
答案解析收藏纠错 + 选题
27. (2023·隆昌模拟) 阅读下列材料：
我们知道 $\text{[math]}$ 的几何意义是在数轴上数x对应的点与原点的距离；即 $\text{[math]}$ ；这个结论可以推广为 $\text{[math]}$ 表示在数轴上数 $\text{[math]}$ ， $\text{[math]}$ 对应点之间的距离.绝对值的几何意义在解题中有着广泛的应用：

例1：解方程 $\text{[math]}$ .

容易得出，在数轴上与原点距离为4的点对应的数为±4，即该方程的 $\text{[math]}$ ±4；

例2：解方程 $\text{[math]}$ .

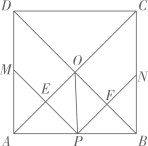
由绝对值的几何意义可知，该方程表示求在数轴上与-1和2的距离之和为5的点对应的x的值.在数轴上，-1和2的距离为3，满足方程的x对应的点在2的右边或在-1的左边.若x对应的

点在2的右边，如图可以看出 $\text{[math]}$ ；同理，若x对应点在-1的左边，可得 $\text{[math]}$ .所以原方程的解是 $\text{[math]}$ 或 $\text{[math]}$ .

例3：解不等式 $\text{[math]}$ .

在数轴上找出 $\text{[math]}$ 的解，即到1的距离为3的点对应的数为-2，4，如图，在-2的左边或在4的右边的 $\text{[math]}$ 值就满足 $\text{[math]}$ ，所以 $\text{[math]}$ 的解为 $\text{[math]}$ 或 $\text{[math]}$ .

参考阅读材料，解答下列问题：
1. （1）方程 $\text{[math]}$ 的解为；
2. （2）方程 $\text{[math]}$ 的解为；
3. （3）若 $\text{[math]}$ ，求x的取值范围.
答案解析收藏纠错 + 选题
28. (2023·隆昌模拟) 如图，抛物线 $\text{[math]}$ 交x轴于 $\text{[math]}$ ， $\text{[math]}$ 两点，与y轴交于点C，连接 $\text{[math]}$ 、 $\text{[math]}$ ．点P是第一象限内抛物线上的一动点，点P的横坐标为m．
1. （1）求此抛物线的表达式；
2. （2）过点P作 $\text{[math]}$ ，垂足为点N，请用含m的代数式表示线段 $\text{[math]}$ 的长，并求出当m为何值时 $\text{[math]}$ 有最大值，最大值是多少？
3. （3）过点P作 $\text{[math]}$ 轴，垂足为点M， $\text{[math]}$ 交 $\text{[math]}$ 于点Q．试探究点P在运动过程中，是否存在这样的点Q，使得以A，C，Q为顶点的三角形是等腰三角形．若存在，请求出此时点Q的坐标，若不存在，请说明理由．
答案解析收藏纠错 + 选题