河南省南阳市桐柏县2022-2023学年八年级下册6月月考数...

更新时间：2023-08-07 浏览次数：38 类型：月考试卷

一、选择题（每小题3分，共30分）

1. (2023八下·桐柏月考) 据相关资料显示，目前发现的一种新型病毒的直径约为120nm（1nm＝10^-9m），120nm用科学记数法表示是（）

A . 120×10^-9m B . 1.20×10^-9m C . 1.20×10^-7m D . 0.12×10^-6m

答案解析收藏纠错 + 选题
2. (2023八下·桐柏月考) 如图，点E在▱ABCD的对角线AC上，AE＝BE＝AD，∠D＝105°，则∠ACB的度数是（）

A . 45° B . 50° C . 55° D . 60°

答案解析收藏纠错 + 选题
3. (2023八下·桐柏月考) 如图，四边形ABCD的对角线AC，BD相交于点O，且AC⊥BD，则下列条件能判定四边形ABCD是菱形的是（）

A . $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023八下·桐柏月考) 如图，在中国象棋的棋盘上，建立适当的平面直角坐标系，使“帅”的坐标是（2，0），“兵”的坐标为（1，4），那么“车”的坐标是（）

A . （-2，2） B . （-2，1） C . （-1，1） D . （-2，0）

答案解析收藏纠错 + 选题
5. (2023八下·桐柏月考) 如图，E是边长为6的正方形ABCD对角线上的一动点，若四边形EFCG为矩形，则矩形EFCG的周长为（）

A . 6 B . 10 C . 12 D . 无法确定

答案解析收藏纠错 + 选题
6. (2023八下·桐柏月考) 如图，反比例函数 $\text{[math]}$ ）的图象上有一点P，PA⊥x轴于点A，点B在y轴上，△PAB的面积为6，则k的值为（）

A . -12 B . 12 C . 6 D . -6

答案解析收藏纠错 + 选题
7. (2024八下·安顺期末) 物美超市试销一批新款衬衫，一周内销售情况如下表所示，超市经理想要了解哪种型号最畅销，那么他最关注的统计量应该是（）
型号（厘米）
38
39
40
41
42
43
数量（件）
13
21
35
48
26
8

A . 平均数 B . 众数 C . 中位数 D . 方差

答案解析收藏纠错 + 选题
8. (2023八下·桐柏月考) 已知关于x的分式方程 $\text{[math]}$ 的解是负数，则n的取值范围为（）

A . n＞1且 $\text{[math]}$ B . n＞1 C . n＜2且 $\text{[math]}$ D . n＜2

答案解析收藏纠错 + 选题
9. (2023八下·桐柏月考) 如图，在▱ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E．若AE＝8，AB＝5，则BF的长为（）

A . 5 B . 6 C . 8 D . 12

答案解析收藏纠错 + 选题
10. (2023八下·桐柏月考) 如图1，在矩形ABCD中，动点P从点B出发，沿B→C→D→A方向匀速运动至点A停止．已知点P的运动速度为1cm/s，设点P的运动时间为x（s），△PAB的面积为y（cm²），若y关于x的函数图象如图2所示，则矩形对角线AC的长为（）

A . 5 B . 6 C . 8 D . 10

答案解析收藏纠错 + 选题

二、填空题（每小题3分，共15分）

11. (2023九上·垫江县月考) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
12. (2023八下·桐柏月考) 关于x的方程 $\text{[math]}$ 有增根，则m的值为．

答案解析收藏纠错 + 选题
13. (2023八下·桐柏月考) 有6个数据的平均数为25，另有9个数据的平均数是20，那么所有这15个数据的平均数是．

答案解析收藏纠错 + 选题
14. (2023八下·桐柏月考) 已知点P（3，y₁），Q（-2，y₂）在一次函数y＝（-4m+1）x+2的图象上，若y₁＜y₂ ，则实数m的取值范围是．

答案解析收藏纠错 + 选题
15. (2023八下·桐柏月考) 如图，在四边形ABCD中，AB∥CD，BC⊥CD，AB＝8cm，DC＝10cm，E是DC上一点，且DE＝3，P从A点出发以1cm/s的速度向B点运动，同时Q从D点出发以2cm/s的速度向C点运动，当其中一点到达终点时，另一点也随之停止，设运动时间为t（s），当t＝时，以A、P、E、Q为顶点的四边形是平行四边形．

答案解析收藏纠错 + 选题

三、解答题（共8小题）

16. (2023八下·桐柏月考)
1. （1）解分式方程： $\text{[math]}$ ；
2. （2）先化简 $\text{[math]}$ ，再从-2，-1，0，1，2中选取一个合适的数作为m的值代入求值．
答案解析收藏纠错 + 选题
17. (2024八下·茅箭月考) 如图，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，垂足分别为点 $\text{[math]}$ ， $\text{[math]}$ .
1. （1）请你只添加一个条件（不另加辅助线），使得四边形 $\text{[math]}$ 为平行四边形，你添加的条件是；
2. （2）添加了条件后，证明四边形 $\text{[math]}$ 为平行四边形.
答案解析收藏纠错 + 选题

18. (2023八下·桐柏月考) 某水果批发商以5元/kg的成本价新进500箱库尔勒香梨，每箱质量10kg，在出售香梨前，需要去掉损坏的香梨，现随机抽取20箱，去掉损坏香梨后称得每箱的质量（单位：kg）如下：

9.7	9.8	9.6	9.5	9.8	9.9	9.8	9.7	9.8	9.7
9.8	9.9	9.7	9.8	9.5	9.7	9.7	9.9	9.7	10.0

整理数据：

质量（kg）	9.5	9.6	9.7	9.8	9.9	10.0
数量（箱）	2	1	7	a	3	1

分析数据：

平均数	众数	中位数
9.75	b	c

（1）直接写出上述表格中a＝，b＝，c＝．
（2）按样本平均数估算这500箱香梨共损坏了多少千克？
（3）根据（2）中的结果，问该水果批发商销售这批香梨每千克售价至少定为多少元才不亏本？（结果保留一位小数）

答案解析收藏纠错 + 选题

19. (2023八下·桐柏月考) 如图，四边形ABCD的对角线AC，BD相交于点O，四边形OBEC是矩形，△BOC≌△DOA．
1. （1）求证：四边形ABCD是菱形．
2. （2）若BC＝13，AC＝24，求菱形ABCD的面积．
答案解析收藏纠错 + 选题
20. (2023八下·桐柏月考) 如图，一次函数y₁＝k₁x+b的图象与反比例函数 $\text{[math]}$ 的图象交于第二象限内的点A（-4，2）和B（-2，m），与x轴交于点C．
1. （1）分别求出这两个函数的表达式．
2. （2）不等式 $\text{[math]}$ 的解集是．
3. （3）在坐标平面内是否存在点P，使得由点O，B，C，P组成的四边形是平行四边形？若存在，请直接写出点P的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题
21. (2023八下·桐柏月考) 如图，在矩形ABCD中，点M是边AD的中点，点P是边BC上的动点，PE⊥MC，PF⊥BM，垂足为点E，F．
1. （1）当矩形ABCD的长与宽满足什么条件时，四边形PEMF为矩形？证明你的结论；
2. （2）如果四边形PEMF为矩形，那么当点P运动到什么位置时，矩形PEMF变为正方形？能证明你的猜想吗？
答案解析收藏纠错 + 选题
22. (2023八下·桐柏月考) 今年的冬奥会点燃了青少年的“冰雪热”，推动了冰雪产业经济．某体育运动器材商店的滑雪护目镜和滑雪头盔成了热销商品．已知滑雪头盔比滑雪护目镜的进价高50元，商店用4000元购进的滑雪头盔与用3000元购进的滑雪护目镜数量一样多．
1. （1）求滑雪护目镜和滑雪头盔的进价；
2. （2）该商店计划购进滑雪护目镜和滑雪头盔共200个，且滑雪护目镜的数量不少于滑雪头盔的2倍．购进后，滑雪护目镜按高于进价18%定价，滑雪头盔按高于进价15%定价．假设该商店购进的这两种商品最后均能按定价售出，请你求出该商店能获得最大利润的进货方案．
答案解析收藏纠错 + 选题
23. (2023八下·桐柏月考) 如图1，在Rt△EAF中，∠A＝90°，∠AEF，∠AFE的外角平分线交于点C，过点C分别作直线AB，AD的垂线，B，D为垂足．
1. （1）【问题发现】
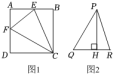
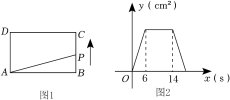
  ∠ECF＝°（直接写出结果，不写解答过程）．
2. （2）【问题探究】
  ①求证：四边形ABCD是正方形．
  ②若AF＝DF＝4，求BE的长．
3. （3）【问题拓展】
  如图2，在△PQR中，∠QPR＝45°，高PH＝4，HR＝1，则HQ的长度是（直接写出结果，不写解答过程）．
答案解析收藏纠错 + 选题