 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
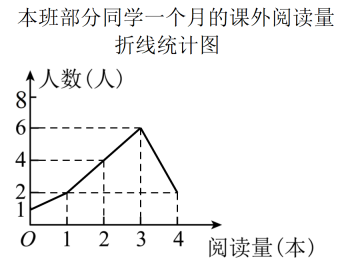
 B .
B . 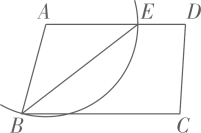 C .
C . 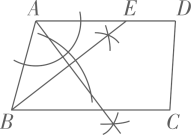 D .
D . 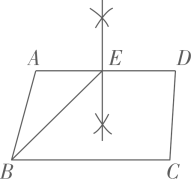
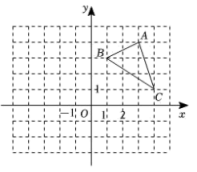
①当x>2时,y随x的增大而减小;②若图象经过点(0,1),则-1<a<0;
③若(-2022,y1),(2022,y2)是函数图象上的两点,则y1<y2:
④若图象上两点对一切正数n,总有y1>y2 , 则
.
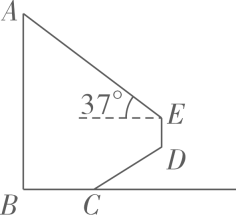
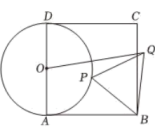
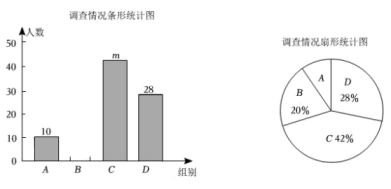
材料2已知实数m,n满足m2-m-1=0,n2-n-1=0,且m≠n,显然m,n是方程x2-x-1=0的两个不相等的实数根,由韦达定理可知m+n=1,mn=-1.
根据上述材料,解决以下问题:
x(元/件) | 40 | 50 | 60 |
y(件) | 10000 | 9500 | 9000 |
