
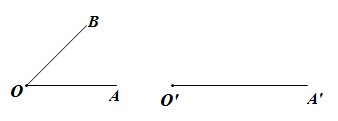
⑴作射线 ;
⑵以O为圆心,任意长为半径作弧,交 于C,交
于D;
⑶以 为圆心,
为半径作弧,交
于
;
⑷以 为圆心,
为半径作弧,交前面的弧于
;
⑸连接 作射线
则
就是所求作的角.
以上作法中,错误的一步是( )

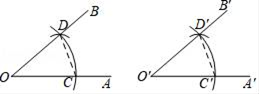

①分别以B,C为圆心,c,b为半径作弧,两弧交于点A;
②作直线 ,在
上截取
;
③连接 ,
,
为所求作的三角形.
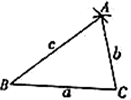

求作: ,使
,
,(用尺规作图,保留作图痕迹,不写作法).
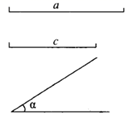
请你根据所学的知识,说明尺规作图作出 ,用到的是三角形全等判定定理中的_▲_,作出的
是唯一的,依据是三角形全等判定定理中的_▲_.


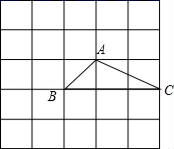
①延长BC到点D,使CD=BC;
②延长CA到点E,使AE=2CA;
③连接AD,BE并猜想线段 AD与BE的大小关系;