2023-2024学年初中数学八年级上册 17.4 一元二次...

更新时间：2023-07-28 浏览次数：37 类型：同步测试

一、选择题

1. (2023八下·江州期末) 某商场销售一种商品，原销售价为100元，为减少库存，经过两次降价，现销售价为81元，如果每次降价率都为x，则根据题意所列的方程正确的是（）.

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023·无锡) 2020年一2022年无锡居民人均可支配收入由5.76万元增长至6.58万元，设人均可支配收入的平均增长率为x，下列方程正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023·富锦模拟) 某校“研学”活动小组在一次野外实践时，发现一种植物的 $\text{[math]}$ 个主干上长出 $\text{[math]}$ 个枝干，每个枝干上再长出 $\text{[math]}$ 个小分支 $\text{[math]}$ 若在一个主干上的主干，枝干和小分支的数量之和是 $\text{[math]}$ 个，则 $\text{[math]}$ 等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023八下·江北期末) 某放射性元素经2天后，质量衰变为原来的 $\text{[math]}$ ．若设这种放射性元素质量的日平均减少率为 $\text{[math]}$ ，则可列出方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023八下·定远期中) 为响应国家“双减政策”，某校2021年第三季度平均每周作业时长为600分钟，经过2021年第四季度和2022年第一季度两次整改后，平均每周作业时长为350分钟．设每季度平均每周作业时长的下降率为a，则可列方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023八下·包河期中) 某商品一月份售价100元，二月份涨价 $\text{[math]}$ ，三月份再次涨价 $\text{[math]}$ 后售价132元，下列所列方程正确的是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023八下·北京市期中) 如图，《九章算术》中的“折竹抵地”问题：今有竹高一丈，末折抵地，去高六尺，折高者几何？意思是：一根竹子，原高一丈（一丈＝十尺），一阵风将竹子折断，竹梢恰好抵地，抵地处离竹子底部6尺远，求折断处离地面的高度．设竹子折断处离地面x尺，根据题意，可列方程为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2020九上·遵化期末) 已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是1，3，4中的任意一个数（ $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 互不相等），当方程 $\text{[math]}$ 的解均为整数时，以1，3和此方程的所有解为边长能构成的多边形一定是（）

A . 轴对称图形 B . 中心对称图形 C . 轴对称图形或中心对称图形 D . 非轴对称图形或中心对称图形

答案解析收藏纠错 + 选题

二、填空题

9. (2023·无锡) 《九章算术》中提出了如下问题：今有户不知高、广，竿不知长短，横之不出四尺，从之不出二尺，邪之适出，问户高、广、邪各几何？这段话的意思是：今有门不知其高宽：有竿，不知其长短，横放，竿比门宽长出4尺：竖放，竿比门高长出2尺：斜放，竿与门对角线恰好相等．问门高、宽和对角线的长各是多少？则该问题中的门高是尺．

答案解析收藏纠错 + 选题
10. (2023八下·蒙城期中) 某学校生物兴趣小组在该校空地上围了一块面积为200m²的矩形试验田，用来种植蔬菜．如图，试验田一面靠墙，墙长35m，另外三面用49m长的篱围成，其中一边开有一扇1m宽的门（不包括篱笆）．设试验田垂直于墙的一边AB的长为xm，则所列方程为__ ．

答案解析收藏纠错 + 选题
11. (2023八下·包河期中) 在学校劳动实践基地里有一块长20米、宽10米的长方形菜地，为了管理方便，准备沿平行于两边的方向纵、横开辟三条等宽的小道（如图中阴影部分所示），剩下部分种植蔬菜，已知种植蔬菜的面积为171平方米，则小道的宽为米．

答案解析收藏纠错 + 选题
12. (2023·邵阳) 某校截止到 $\text{[math]}$ 年底，校园绿化面积为 $\text{[math]}$ 平方米．为美化环境，该校计划 $\text{[math]}$ 年底绿化面积达到 $\text{[math]}$ 平方米．利用方程想想，设这两年绿化面积的年平均增长率为 $\text{[math]}$ ，则依题意列方程为．

答案解析收藏纠错 + 选题
13. (2023七下·顺义期中) 有一个正方形的花园，如果它的边长增加 $\text{[math]}$ ，那么花园面积将增加 $\text{[math]}$ ，则原花园的面积为．

答案解析收藏纠错 + 选题

三、解答题

14. (2022八下·临淄期中) 如图，在直角梯形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．动点 $\text{[math]}$ 从点 $\text{[math]}$ 出发，沿射线 $\text{[math]}$ 的方向以每秒2个单位的速度运动，动点 $\text{[math]}$ 从点 $\text{[math]}$ 出发，沿射线 $\text{[math]}$ 的方向以每秒1个单位的速度向点 $\text{[math]}$ 运动，点 $\text{[math]}$ ， $\text{[math]}$ 分别从点 $\text{[math]}$ ， $\text{[math]}$ 同时出发，当点 $\text{[math]}$ 运动到点 $\text{[math]}$ 时，点 $\text{[math]}$ 随之停止运动．设运动的时间为 $\text{[math]}$ （秒），当 $\text{[math]}$ 为何值时，以 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三点为顶点的三角形是等腰三角形？

答案解析收藏纠错 + 选题

15. (2023八下·嘉兴期末) 嘉海学校八年级开展社会实践活动，下表是“遇数临风”小组的记录表，请根据相关信息解决表中的两个问题．

嘉海学校社会实践记录表
团队名称	遇数临风	活动时间	$\text{[math]}$
班级人员	$\text{[math]}$ 王嘉、马俊、张宁	地点	城南蔬菜超市
实践内容	调查青菜行情，帮超市解决销售问题的同时为顾客谋实惠．
调研信息	青菜的进价为2元/千克．
	青菜售价为 $\text{[math]}$ 元/千克时，每天可销售 $\text{[math]}$ 千克．
	每千克每涨价 $\text{[math]}$ 元，每天少销售5千克．
解决问题	问题1	某天超市正好销售 $\text{[math]}$ 千克的青菜，则获利多少元？
	问题2 若超市想一天销售青菜获利 $\text{[math]}$ 元，则青菜的售价为多少元/千克？

答案解析收藏纠错 + 选题

四、综合题

16. (2022九上·莒南期中) 如图，在 $\text{[math]}$ ABC中，∠B＝90°，AB=6cm，AC=10cm，点P从点A开始沿AB向点B以1cm/s的速度移动，点Q从B点开始沿BC向点C以2cm/s的速度移动，P、Q两点同时出发，当一个点到达终点时另一个点也随之停止运动，运动时间为t．
1. （1）几秒后四边形APQC的面积是19平方厘米；
2. （2）若用S表示四边形APQC的面积，经过多长时间S取得最小值，并求出S的最小值．
答案解析收藏纠错 + 选题
17. (2020·山西模拟) 阅读下列材料，并完成相应的任务．
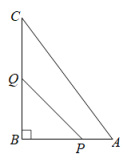
古希腊的几何学家海伦在他的著作《度量论》一书中给出了利用三角形三边之长求面积的公式﹣﹣﹣﹣海伦公式S＝ $\text{[math]}$ （其中a ， b ， c是三角形的三边长， $\text{[math]}$ ，S为三角形的面积），并给出了证明

例如：在△ABC中，a＝3，b＝4，c＝5，那么它的面积可以这样计算：

∵a＝3，b＝4，c＝5

∴ $\text{[math]}$ ＝6

∴S＝ $\text{[math]}$ ＝ $\text{[math]}$ ＝6

事实上，对于已知三角形的三边长求三角形面积的问题，还可用我国南宋时期数学家秦九韶提出的秦九韶公式等方法解决．

根据上述材料，解答下列问题：

如图，在△ABC中，BC＝7，AC＝8，AB＝9
1. （1）用海伦公式求△ABC的面积；
2. （2）如图，AD、BE为△ABC的两条角平分线，它们的交点为I ，求△ABI的面积．
答案解析收藏纠错 + 选题