2023年四川省中考数学真题分类汇编：锐角三角函数、投影与视...

更新时间：2023-07-30 浏览次数：76 类型：二轮复习

一、选择题

1. (2023·广元) 某几何体是由四个大小相同的小立方块拼成，其俯视图如图所示，图中数字表示该位置上的小立方块个数，则这个几何体的左视图是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
2. 一个立体图形的三视图如图所示，则该立体图形是（）

A . 圆柱 B . 圆锥 C . 长方体 D . 三棱柱

答案解析收藏纠错 + 选题
3. (2023·内江) 如图是由5个完全相同的小正方体堆成的物体，其主视图是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2023·广安) 如图，由5个大小相同的小正方体搭成的几何体，它的俯视图是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2024九下·浦北月考) 如图，小兵同学从 $\text{[math]}$ 处出发向正东方向走 $\text{[math]}$ 米到达 $\text{[math]}$ 处，再向正北方向走到 $\text{[math]}$ 处，已知 $\text{[math]}$ ，则 $\text{[math]}$ ， $\text{[math]}$ 两处相距（）

A . $\text{[math]}$ 米 B . $\text{[math]}$ 米 C . $\text{[math]}$ 米 D . $\text{[math]}$ 米

答案解析收藏纠错 + 选题
6. 由相同的小正方体搭成的立体图形的部分视图如图所示，则搭成该立体图形的小正方体的最少个数为（）

A . 6 B . 9 C . 10 D . 14

答案解析收藏纠错 + 选题
7. (2023·遂宁) 生活中一些常见的物体可以抽象成立体图形，以下立体图形中三视图形状相同的可能是（）

A . 正方体 B . 圆锥 C . 圆柱 D . 四棱锥

答案解析收藏纠错 + 选题
8. 如图是由4个相同的小立方体堆成的几何体的俯视图，小正方形中的数字表示该位置小立方体的个数，则这个几何体的主视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
9. (2023·自贡) 如图中六棱柱的左视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题

二、填空题

10. (2024九下·黄石月考) 一渔船在海上A处测得灯塔C在它的北偏东60°方向，渔船向正东方向航行12海里到达点B处，测得灯塔C在它的北偏东45°方向，若渔船继续向正东方向航行，则渔船与灯塔C的最短距离是海里．

答案解析收藏纠错 + 选题
11. (2023·成都) 一个几何体由几个大小相同的小立方块搭成，它的主视图和俯视图如图所示，则搭成这个几何体的小立方块最多有个.

答案解析收藏纠错 + 选题

三、解答题

12. (2023·遂宁) 某实践探究小组想测得湖边两处的距离，数据勘测组通过勘测，得到了如下记录表：

实践探究活动记录表
活动内容测量湖边A、B两处的距离
成员组长：××× 组员：××××××××××××
测量工具测角仪，皮尺等
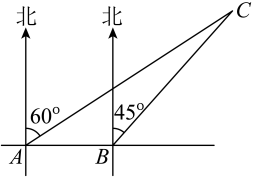
测量示意图		说明：因为湖边A、B两处的距离无法直接测量，数据勘测组在湖边找了一处位置C．可测量C处到A、B两处的距离．通过测角仪可测得 $\text{[math]}$ 的度数．
测量数据	角的度数	$\text{[math]}$
		$\text{[math]}$
		$\text{[math]}$
	边的长度	$\text{[math]}$ 米
		$\text{[math]}$ 米

数据处理组得到上面数据以后做了认真分析．他们发现不需要勘测组的全部数据就可以计算出A、B之间的距离．于是数据处理组写出了以下过程，请补全内容．

（1）
已知：如图，在 $\text{[math]}$ 中， $\text{[math]}$ ． ____．（从记录表中再选一个条件填入横线）

求：线段 $\text{[math]}$ 的长．（为减小结果的误差，若有需要， $\text{[math]}$ 取 $\text{[math]}$ ， $\text{[math]}$ 取 $\text{[math]}$ ， $\text{[math]}$ 取 $\text{[math]}$ 进行计算，最后结果保留整数．）

答案解析收藏纠错 + 选题

13. (2023·宜宾) 渝昆高速铁路的建成，将会显著提升宜宾的交通地位．渝昆高速铁路宜宾临港长江公铁两用大桥（如图 $\text{[math]}$ ），桥面采用国内首创的公铁平层设计．为测量左桥墩底到桥面的距离 $\text{[math]}$ ，如图 $\text{[math]}$ ．在桥面上点 $\text{[math]}$ 处，测得 $\text{[math]}$ 到左桥墩 $\text{[math]}$ 的距离 $\text{[math]}$ 米，左桥墩所在塔顶 $\text{[math]}$ 的仰角 $\text{[math]}$ ，左桥墩底 $\text{[math]}$ 的俯角 $\text{[math]}$ ，求 $\text{[math]}$ 的长度．（结果精确到 $\text{[math]}$ 米．参考数据： $\text{[math]}$ ， $\text{[math]}$ ）

答案解析收藏纠错 + 选题
14. (2024九下·乌鲁木齐模拟) 为建设美好公园社区，增强民众生活幸福感，某社区服务中心在文化活动室墙外安装遮阳篷，便于社区居民休憩.
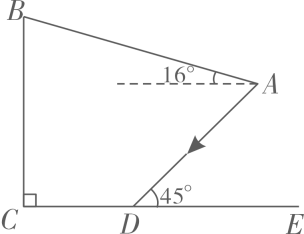
如图，在侧面示意图中，遮阳篷AB长为5米，与水平面的夹角为16°，且靠墙端离地高BC为4米，当太阳光线AD与地面CE的夹角为45°时，求阴影CD的长.（结果精确到0.1米；参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

答案解析收藏纠错 + 选题
15. (2023·泸州) 如图，某数学兴趣小组为了测量古树 $\text{[math]}$ 的高度，采用了如下的方法：先从与古树底端 $\text{[math]}$ 在同一水平线上的点A出发，沿斜面坡度为 $\text{[math]}$ 的斜坡 $\text{[math]}$ 前进 $\text{[math]}$ 到达点 $\text{[math]}$ ，再沿水平方向继续前进一段距离后到达点 $\text{[math]}$ ．在点 $\text{[math]}$ 处测得古树 $\text{[math]}$ 的顶端 $\text{[math]}$ 的俯角为 $\text{[math]}$ ，底部 $\text{[math]}$ 的俯角为 $\text{[math]}$ ，求古树 $\text{[math]}$ 的高度（参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，计算结果用根号表示，不取近似值）．

答案解析收藏纠错 + 选题

四、综合题

16. (2023·广元) “一缕清风银叶转”，某市20台风机依次矗立在云遮雾绕的山脊之上，风叶转动，风能就能转换成电能，造福千家万户．某中学初三数学兴趣小组，为测量风叶的长度进行了实地测量．如图，三片风叶两两所成的角为 $\text{[math]}$ ，当其中一片风叶 $\text{[math]}$ 与塔干 $\text{[math]}$ 叠合时，在与塔底D水平距离为60米的E处，测得塔顶部O的仰角 $\text{[math]}$ ，风叶 $\text{[math]}$ 的视角 $\text{[math]}$ ．
1. （1）已知α，β两角和的余弦公式为： $\text{[math]}$ ，请利用公式计算 $\text{[math]}$ ；
2. （2）求风叶 $\text{[math]}$ 的长度．
答案解析收藏纠错 + 选题
17. (2023·自贡) 为测量学校后山高度，数学兴趣小组活动过程如下：
1. （1）测量坡角
  如图1，后山一侧有三段相对平直的山坡 $\text{[math]}$ ，山的高度即为三段坡面的铅直高度 $\text{[math]}$ 之和，坡面的长度可以直接测量得到，要求山坡高度还需要知道坡角大小．
  如图2，同学们将两根直杆 $\text{[math]}$ 的一端放在坡面起始端A处，直杆 $\text{[math]}$ 沿坡面 $\text{[math]}$ 方向放置，在直杆 $\text{[math]}$ 另一端N用细线系小重物G，当直杆 $\text{[math]}$ 与铅垂线 $\text{[math]}$ 重合时，测得两杆夹角 $\text{[math]}$ 的度数，由此可得山坡AB坡角 $\text{[math]}$ 的度数．请直接写出 $\text{[math]}$ 之间的数量关系．
2. （2）测量山高
  同学们测得山坡 $\text{[math]}$ 的坡长依次为40米，50米，40米，坡角依次为 $\text{[math]}$ ；为求 $\text{[math]}$ ，小熠同学在作业本上画了一个含 $\text{[math]}$ 角的 $\text{[math]}$ （如图3），量得 $\text{[math]}$ ．求山高 $\text{[math]}$ ．（ $\text{[math]}$ ，结果精确到1米）
3. （3）测量改进
  由于测量工作量较大，同学们围绕如何优化测量进行了深入探究，有了以下新的测量方法．
  
  如图4，5，在学校操场上，将直杆NP置于 $\text{[math]}$ 的顶端，当 $\text{[math]}$ 与铅垂线 $\text{[math]}$ 重合时，转动直杆 $\text{[math]}$ ，使点N，P，D共线，测得 $\text{[math]}$ 的度数，从而得到山顶仰角 $\text{[math]}$ ，向后山方向前进40米，采用相同方式，测得山顶仰角 $\text{[math]}$ ；画一个含 $\text{[math]}$ 的直角三角形，量得该角对边和另一直角边分别为 $\text{[math]}$ 厘米， $\text{[math]}$ 厘米，再画一个含 $\text{[math]}$ 的直角三角形，量得该角对边和另一直角边分别为 $\text{[math]}$ 厘米， $\text{[math]}$ 厘米．已知杆高MN为 $\text{[math]}$ 米，求山高 $\text{[math]}$ ．（结果用不含 $\text{[math]}$ 的字母表示）
答案解析收藏纠错 + 选题