测试者 | 平均成绩 | 方差 |
甲 | 6.3 | 0.21 |
乙 | 6.0 | 0.59 |
丙 | 5.7 | 0.12 |
丁 | 6.3 | 0.35 |
若从其中选出1名成绩好且发挥稳定的同学参加学校运动会,则应选( )
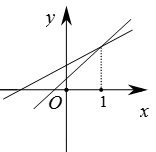 B .
B . 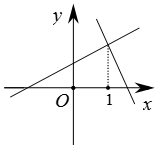 C .
C . 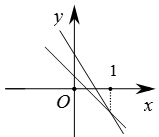 D .
D . 
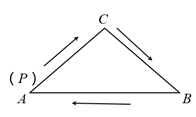
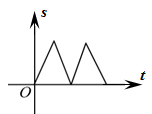 B .
B . 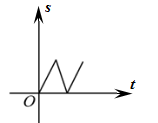 C .
C . 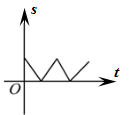 D .
D . 
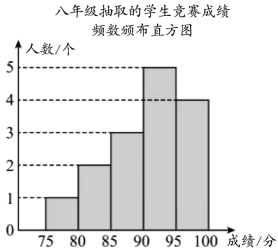
下面给出了部分信息:
七年级15个学生的竞赛成绩:78,83,89,97,98,85,100,94,87,90,93,92,99,95,100
八年级15个学生的竞赛成绩中D等级包含的所有数据为:91,92,94,90,93
七、八年级中各随机抽取15名学生的竞赛成绩统计表
|
年级 |
平均数 |
众数 |
中位数 |
方差 |
|
七年级 |
92 |
a |
93 |
41.7 |
|
八年级 |
92 |
87 |
b |
50.2 |
|
车型 |
|
|
|
大货车 |
|
|
|
小货车 |
|
|
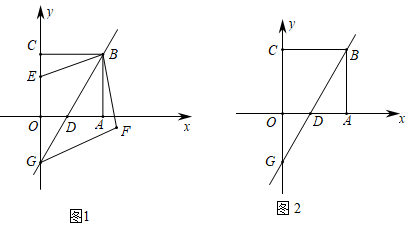
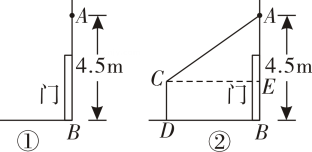
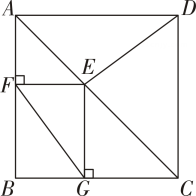
①当四边形BEGF为菱形时,求点E的坐标;
②若N为平面内一点,当以B , E , F , N为顶点的四边形为矩形时,m的值为 . (请直接写出答案)