 B .
B .  C .
C .  D .
D . 

 B .
B .  C .
C .  D .
D . 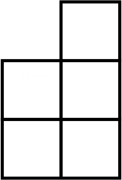



 B .
B .  C .
C .  D .
D . 




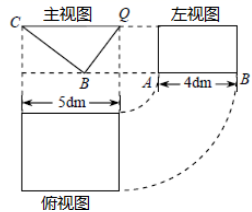
测量方法如下:在地面上找一点D,用测角仪测出看旗杆AB顶B的仰角为67.4°,沿DE方向走4.8米到达C地,再次测得看旗杆顶B的仰角为73.5°.



①图2为徐州狮子山楚王墓出土的“雷纹玉环”及其主视图,试判断该件玉器的比例关系是否符合“肉好若一”?
②图3表示一件圆形玉坯,若将其加工成玉璧,且比例关系符合“肉倍好”,请画出内孔.
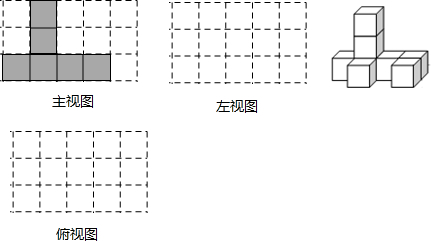
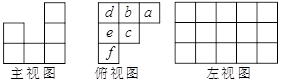


①图3是小刘制作的模型中正方体六个面的展开图,图中缺失的有一部分已经很用阴影表示,请你用阴影表示出其余缺失部分,并标出边的长度.
②如果把小刘的模型中正方体的六个面展开,则展开图的周长是 ▲ cm;请你在图方格中画出小刘的模型中正方体六个面的展开图周长最大时的图形.
