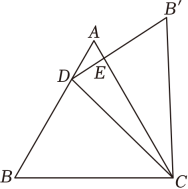
 B .
B .  C .
C .  D .
D . 

![]()
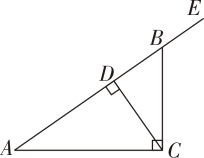
对于上述问题,在以下解答过程的空白处填上适当的内容(理由或数学式).
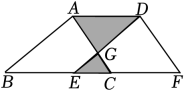
解:(1)CD⊥AB(已知),
∴∠CDB= ▲ .
∵∠EBC=∠CDB+∠BCD ▲ ,
∴∠EBC= ▲ +35°= ▲ (等量代换)(2)∵∠EBC=∠A+∠ACB( )
∴∠A=∠EBC-∠ACB(等式的性质)
∵∠ACB=90°(已知),
∴∠A= ▲ -90°= ▲ (等量代换).
你还能用其他方法解决这一问题吗?
我们知道每一个二元一次方程都有无数组解,例如……都是方程x+2y=5的解,但在实际生活中我们往往只需求出其正整数解即可.
我们在求一个二元一次方程的正整数解时通常采用如下方法:
例:求2x+5y=24这个二元一次方程的正整数解.
解:由2x+5y=24,得: ,
根据x、y为正整数,运用尝试法可以知道
方程2x+5y=24的正整数解为 或
.
问题:
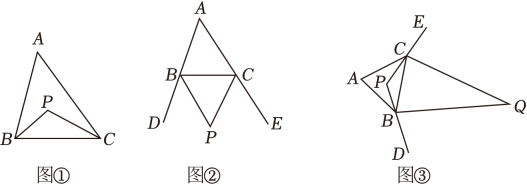
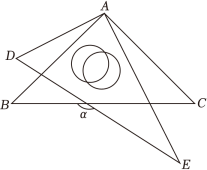
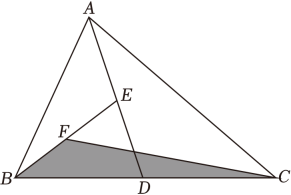
如图①,在△ABC中,BP平分∠ABC,CP平分∠ACB,请你判断∠A和∠P间的数量关系并说明理由.
刘华对这个问题进行了判断并给出了证明过程,下面是部分证明过程,请你补全余下的证明过程.
解:结论:∠P=_ .
理由:∵BP平分∠ABC,CP平分∠ACB,
∴∠PBC=∠ABC,∠PCB=
∠ACB.
∴∠P=180°-∠PBC-∠PCB.
=180°-(∠ABC+∠ACB)
=180°-(180°-∠A)
=_

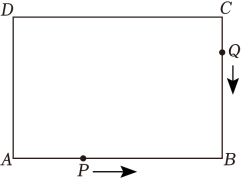
②当点P在BC上运动时,BP=cm.(用含t的代数式表示)