 B .
B .  C .
C .  D .
D . 


若
, 则点
到
的距离为
;
;
点
在
的中垂线上;
若
, 则
.


等式的基本性质;
分式的基本性质;
乘法分配律;
乘法交换律.

⑴将沿
轴方向向左平移
个单位后得到
, 画出
;
⑵将绕
顺时针旋转
后得到
, 画出
, 并写出顶点
,
,
的坐标.
|
思考 我们知道,菱形的对角线互相垂直,反过来,对角线互相垂直的平行四边形是菱形吗? 可以发现并证明菱形的一个判定定理; 对角线互相垂直的平行四边形是菱形. |
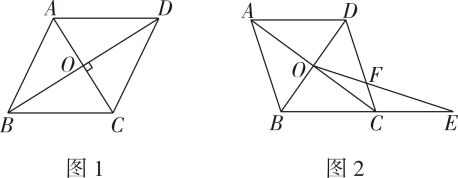
定理证明
已知:在▱中,对角线
, 垂足为
.
求证:▱是菱形.
如图 , 在▱
中,对角线
和
相交于点
,
,
,
.
求证:▱是菱形.
请判断线段
,
,
的数量关系,并根据图
进行证明
提示:过点
作
, 交
与
;
若
, 在点
的移动过程中,当
是等腰三角形时,直接写出此时
的面积.