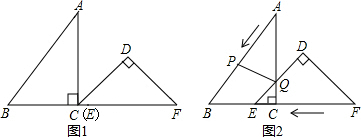
 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
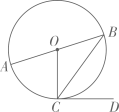
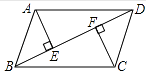
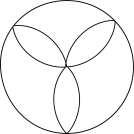
①求的半径;
②设与
边的另一个交点为
, 求线段
,
与劣弧
所围成的阴影部分的面积.(结果保留根号和
)