
 C .
C .  D .
D . 
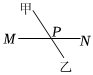 B .
B . 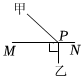 C .
C . 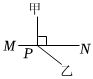 D .
D . 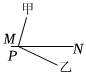
![]()

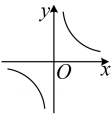 B .
B . 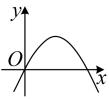 C .
C .  D .
D . 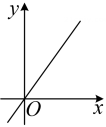
尺寸 | 大 | 中 | 小 |
| | | |
| | | |
烧制一个大尺寸陶艺品的位置可替换为烧制两个中尺寸或六个小尺寸陶艺品,但烧制较小陶艺品的位置不能替换为烧制较大陶艺品.
某批次需要生产个大尺寸陶艺品,
个中尺寸陶艺品,
个小尺寸陶艺品.
定理:在直角三角形中,如果一个锐角等于 | |
方法一 | 方法二 |

|
蔬菜价格 |
众数 |
中位数 |
|
西红柿 |
|
|
|
黄瓜 |
|
|
根据以上信息,回答下列问题:

通过对某只野兔一次跳跃中水平距离单位:
与竖直高度
单位:
进行的测量,得到以下数据:
水平距离 | | | | | | | |
竖直高度 | | | | | | | |
根据上述数据,回答下列问题:野兔本次跳跃的最远水平距离为
, 最大竖直高度为
;
求满足条件的抛物线的解析式;