证明:∵∠C=∠CDE
∴ ①
∵∠BDC = 90°
∴∠BDF +∠CDF = 90°,∠C +∠DBF = 90°
又∠C=∠CDE
∴ ②
∴BF = DF
∴BF=CF=BC
∵AD =BC,
∴ ③
∵ADBC
∴四边形ABFD是平行四边形
∵ ④
∴四边形ABFD是菱形
证明:∵点E是CD的中点,∴CE=DE
∵CH=BH,
∴ ,
∵//
,
∴四边形BDEF是平行四边形
∵//
,
∴
∵DF平分∠BDC,
∴ ∴∠BFD=∠BDF,
∴ ,
∴四边形BDEF是菱形.
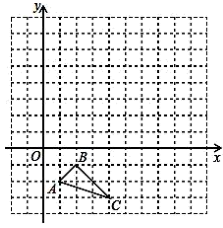
⑴画出关于
轴对称的
;
⑵以点为位似中心,在网格中画出
的位似图形
, 使
与
的相似比为
;
⑶设点为
内一点,则依上述两次变换后点
在
内的对应点
的坐标是 ▲ .
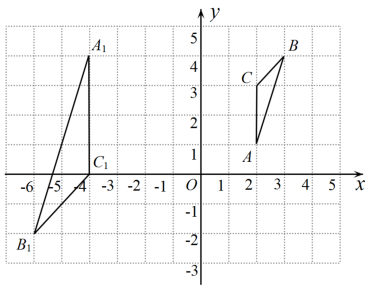

( 1 )画出绕点O顺时针旋转
后得到的
;
( 2 )在y轴的左侧以O为位似中心作的位似图形
, 使新图与原图相似比为
;
( 3 )若点在线段
上,直接写出变化(2)后点D的对应点
的坐标为____.( 4 )分别求出
的周长和
的面积.
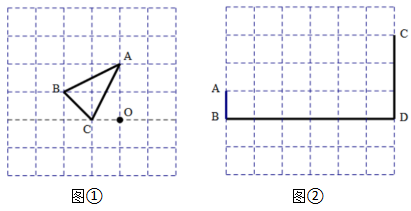


( 1 )画出与关于y轴对称的
;
( 2 )以原点O为位似中心,在第三象限内画一个 , 使它与
的相似比为
, 并写出点
,
,
的坐标.
( 3 )若方格中每个小正方形的边长为1个单位长度,求的面积.
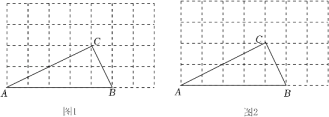

⑴已知与
关于y轴对称,请画出
;
⑵以原点O为位似中心,在x轴上方画出的位似图形
(点A,B,C的对应点分别为点
,
,
),使
与
的位似比为
.