一、选择题:(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一个是正确的,请把正确的选项填入题后的括号内.
-
A . 2,2,4
B . 3,4,8
C . 1,2,3
D . 2,5,6
-
-
A . 30°
B . 40°
C . 50°
D . 60°
-
-
A . 360°
B . 540°
C . 720°
D . 1080°
-
6.
(2024八上·武汉期末)
如图,小明书上的三角形被墨迹污染了一部分,他根据所学的知识很快就画出了一个与书上完全一样的三角形,那么小明画图的依据是( )

A . ASA
B . AAS
C . SAS
D . SSS
-
7.
(2024八下·东坡月考)
如图,点B,E,C,F四点在同一条直线上,AC∥DF,AC =DF,添加一个条件,不能判定△ABC≌△DEF的是( )

A . BE=CF
B . AB=DE
C . ∠B=∠DEF
D . ∠A=∠D
-
8.
(2023八上·襄州期中)
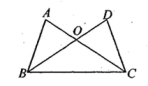
如图,在△ABC中,∠ACB=50°,∠ABC与∠BAC的平分线交于点O,则∠AOB度数为( )

A . 100°
B . 115°
C . 125°
D . 135°
-
A . 12
B . 15
C . 12或15
D . 9
-
10.
(2023八上·襄州期中)
如图,在△ABC中,BO平分∠ABC,CO平分∠ACB,且OM∥AB,ON∥AC,若△OMN的周长是6,则BC的长是( )

A . 6
B . 3
C . 12
D . 9
二、填空题(本大题共6小题,每小题3分,共18分把答案填在相应横线上.)
-
-
-
-
14.
(2023八上·襄州期中)
如图,若点A,B,C,D,E,F是平面上的6个点,则∠A+∠B+∠C+∠D+∠E+∠F的度数是
.

-
15.
(2023八上·襄州期中)
在△ABC中,AB=AC,∠A=120°,AB的垂直平分线分别交AB,BC于D,E,BE=3,则EC的长为
.

-
16.
(2023八上·襄州期中)
如图,将等边△ABC折叠,使点B恰好落在AC边上的点D处,折痕为EF,O为折痕EF上的动点,若AD=2,AC =6,则△OCD的周长最小值为

三、解答题(本大题共9小题,共72分解答应写出文字说明,证明过程或演算步骤)
-
17.
(2023八上·襄州期中)
如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=40,∠2=20°,求∠AEB的度数.

-
-
19.
(2024八上·斗门期末)
如图,在四边形ABCD中,BP,CP分别平分∠ABC和∠BCD,若∠A=90°,∠D=130°,求∠P的度数.

-
20.
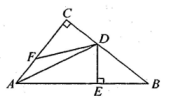
(2023八上·襄州期中)
如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC上,BE=FC.求证:BD=FD.
-
21.
(2023八上·襄州期中)
根据下列要求作(画)图,保留作(画)图痕迹,不写作(画)法.

⑴如图1,作△ABC的角平分线CE;
⑵如图2,在6×6的长方形网格中,每个小正方形的边长为1,小正方形的每一个顶点叫做格点.△ABC的顶点都在格点上.请仅用无刻度直尺画出△ABC的中线CD.(保留画图过程痕迹)
-
22.
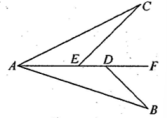
(2023八上·襄州期中)
如图,A,E,D三点在同一直线上,AB=AC,∠BAC=∠BDF=∠CEF.求证:AE=BD.
-
23.
(2023八上·襄州期中)
如图,在△ABC中,∠ACB=90°.点D在△ABC外,连接AD,作DE⊥AB于点E,交BC于点F,AD=AB,AE=AC.

-
-
-
24.
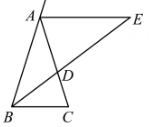
(2023八上·襄州期中)
如图,在△ABC中,AB=AC,∠BAC=36°,BD平分∠ABC交AC于点D.过点A作AE∥BC,交BD的延长线于点E.
-
-
-
(3)
若BC=m,CD=n,求BE的长(用含m,n的式子表示).
-
-
(1)
[特例证明]
如图1,当点E是AB中点时,求证:AE=BD.
-
(2)
[类比探究]
当点E不是AB中点时,判断线段AE与BD的数量关系,并结合图2说明理由.
-
(3)
[拓展运用]
点E在直线AB上运动,当∠DEC=120°时,若BC=2,请直接写出CD的长.
 B .
B .  C .
C .  D .
D .