湖北省襄阳襄州区2023-2024学年九年级上册数学期中试卷

更新时间：2023-12-21 浏览次数：35 类型：期中考试

一、选择题：(本大题共10个小题，每小题3分，共30分)在每小题给出的四个选项中，只有一项是符合题目要求的，请将答案写在括号里．

1. (2023九上·襄州期中) 方程x(x-1)=0的根是（）

A . x=0 B . x=1 C . x₁=0，x₂=1 D . x₁=0，x₂=-1

答案解析收藏纠错 + 选题
2. (2023九上·襄州期中) 下列图案中不是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2023九上·襄州期中) 已知⊙O的半径是4cm，点P与⊙O在同一平面内，OP=3cm，下列结论正确的是（）

A . 点P在⊙O内 B . 点P在⊙O上 C . 点P在⊙O外 D . 不能确定

答案解析收藏纠错 + 选题
4. (2023九上·襄州期中) 如图，将OAOB绕点O按逆时针方向旋转60°后得到△COD，若∠AOB=20°，则∠AOD的度数是（）

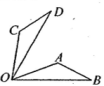
A . 20° B . 40° C . 50° D . 60°

答案解析收藏纠错 + 选题
5. (2024九上·峰峰矿月考) 要得到抛物线y=2(x-4）²-1，可以将抛物线 $\text{[math]}$ （）

A . 向左平移4个单位长度，再向上平移1个单位长度 B . 向左平移4个单位长度，再向下平移1个单位长度 C . 向右平移4个单位长度，再向上平移1个单位长度 D . 向右平移4个单位长度，再向下平移1个单位长度

答案解析收藏纠错 + 选题
6. (2023九上·襄州期中) 如图，在⊙O中， $\text{[math]}$ ，则∠BOC的度数为（）

A . 100° B . 110° C . 120° D . 150°

答案解析收藏纠错 + 选题
7. (2023九上·襄州期中) 某商品原价每件为200元，连续两次降价m%后售价为162元，则m的值为（）

A . 5 B . 10 C . 15 D . 20

答案解析收藏纠错 + 选题
8. (2023九上·襄州期中) 半径为3的圆中，一条弦长为4，则圆心到这条弦的距离是( )

A . 3 B . 4 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2023九上·襄州期中) 点A(-3，y₁)，B( -2，y₂)，C(2，y₃)都在抛物线y=-2(x+1)²-1上，将y₁ ， y₂ ， y₃按从小到大排列并用”<“连接，正确的是（）

A . y₃<y₂<y₁ B . y₁<y₂<y₃ C . y₁<y₃<y₂ D . y₃<y₁<y₂

答案解析收藏纠错 + 选题
10. (2023九上·襄州期中) 抛物线y=ax²+bx+c(a≠0)的图象如图所示，则下列结论错误的是（）

A . b>0 B . b²<4ac C . 2a-b>0 D . a+b+c>0

答案解析收藏纠错 + 选题

二、填空题(本大题共6小题，每小题3分，共18分把答案填在相应横线上 )

11. (2023九上·襄州期中) 在平面直角坐标系中，点( -3，2)关于原点的对称点的坐标是

答案解析收藏纠错 + 选题
12. (2023九上·襄州期中) 一元二次方程x²-6x+m=0有一个根为2，则另一根为

答案解析收藏纠错 + 选题
13. (2023九上·襄州期中) 参加聚会的所有人之间都要互送一张卡片，共送出56张卡片，参加聚会的有人

答案解析收藏纠错 + 选题
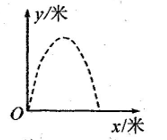
14. (2023九上·襄州期中) 如图，某广场有一喷水池，水从地面喷出，以在水平地面内的一条水平线为x轴，出水点为原点，建立平面直角坐标系，水在空中划出的曲线是抛物线y=-x²+4x(单位：米)的一部分，则水喷出的最大高度是米

答案解析收藏纠错 + 选题
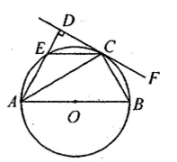
15. (2023九上·襄州期中) 点P为⊙O外一点，PA，PB分别与⊙O相切于点A，B，点C为⊙O上不与A，B重合的点，若∠P=80° ，则∠ACB的度数是

答案解析收藏纠错 + 选题
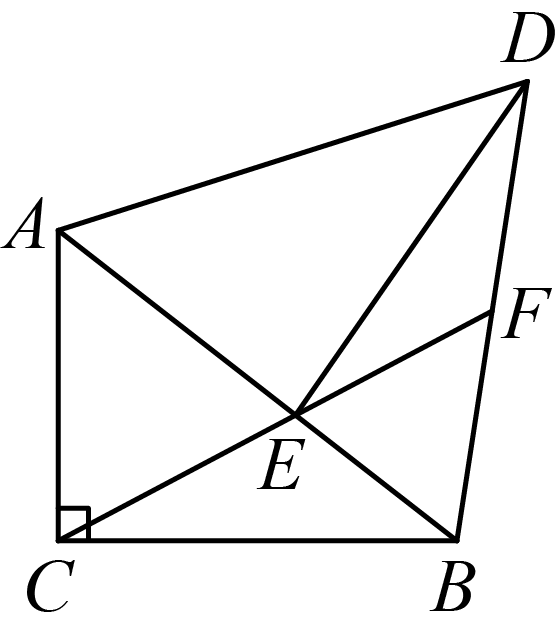
16. (2024·旺苍模拟) 如图，在△ABC中，∠ACB=90°，AC=3，BC=4，将△ABC绕点A旋转，使点C落在AB边上的点E处，点B落在点D处，连接BD，CE，延长CE交BD于点F，则EF的长为

答案解析收藏纠错 + 选题

三、解答题(本大题共9小题，共72分解答应写出文字说明，证明过程或演算步骤． )

17. (2023九上·襄州期中) 用适当的方法解下列方程：
1. （1） (x-2)²-(x-2) =0；
2. （2） x²-x=x+1．
答案解析收藏纠错 + 选题
18. (2023九上·襄州期中) 如图是由小正方形组成的7×6网格，每个小正方形的顶点叫做格点△ABC的顶点都是格点．仅用无刻度的直尺在给定网格中完成画图．
1. （1）请在图1中画出△ABC绕点A顺时针旋转90°后得到的△AB₁C₁；
2. （2）请在图2中画出△ABC的外接圆的圆心O．(保留画图过程痕迹).
答案解析收藏纠错 + 选题
19. (2023九上·襄州期中) 抛物线y=x²-2mx+m²-1与y轴交于点(0，3)，且顶点在第四象限．
1. （1）求该抛物线的解析式；
2. （2）请直接写出当0≤x≤3时，y的取值范围
答案解析收藏纠错 + 选题
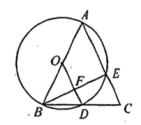
20. (2023九上·襄州期中) 如图，在△ABC中，AB=AC，以AB为直径的⊙O分别交BC，AC于点D，E，连接EB，交OD于点F．
1. （1）求证：OD⊥BE；
2. （2）若EF=4，DF=2，求⊙O的半径
答案解析收藏纠错 + 选题
21. (2023九上·襄州期中) 关于x的一元二次方程x²-2mx+m²+m-3=0有实数根．
1. （1）求m的范围；
2. （2）如果方程两根分别为α，β，若αβ=17，求m的值
答案解析收藏纠错 + 选题
22. (2023九上·襄州期中) 如图，AB是⊙O的直径，点C，E在⊙O上，AC平分∠BAE，CD⊥AE交AE的延长线于点D．
1. （1）求证：CD是⊙O的切线；
2. （2）连接EC，若DE=1，AE=2，求EC的长．
答案解析收藏纠错 + 选题
23. (2023九上·襄州期中) 某批发商出售一种成本价为10元/件的商品，市场调查发现，该商品每周的销售量y(件)与销售价x(元/件)满足一次函数y=-10x+400．这种商品每周的销售利润为w元
1. （1）求w与x的函数关系式；
2. （2）该商品销售价定为每件多少元时，每周的销售利润最大？
3. （3）商家为了盘活资金，碱少库存，要确保这种商品每周的销售量不少于180件，若这种商品每周的销售利润为2000元，则该商品每周的销售量是多少？
答案解析收藏纠错 + 选题
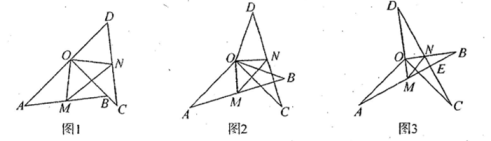
24. (2023九上·襄州期中) 在△AOB中，OA>OB，将△AOB绕点O逆时针旋转90°得到△COD，点M，N分别是AB，CD的中点，连接OM，ON，MN．
1. （1）证明与推断：如图1，当∠AOB=90°时，①求证：△AOM≌△CON；②推断：△MON是三角形；
2. （2）类比探究：如图2，当∠AOB>90°时，判断△MON的形状并证明；
3. （3）拓展运用：在(2)的条件下，当点N在OB上时(如图3)，设AB，CD相交于点E，若AM= $\text{[math]}$ MN，OB=3，求线段MN的长．
答案解析收藏纠错 + 选题
25. (2023九上·襄州期中) 如图，抛物线y=ax²+bx-3与x轴交于A(-1，0)，B(3，0)两点，与y轴交于点C．
1. （1）求抛物线的解析式及点C的坐标；
2. （2）若点P在直线BC下方的抛物线上，过点P作PD∥OC交BC于点D，求PD长度的最大值；
3. （3）当-1≤x≤m时，y的最大值与最小值的和是-2，求m的值
答案解析收藏纠错 + 选题