四川省广元市旺苍县2024年中考一模数学试卷

更新时间：2024-05-09 浏览次数：39 类型：中考模拟

一、单选题（下列每小题给出的四个选项中，只有一个是符合题意的．每小题3分，共30分）

1. (2024九上·南康月考) 用配方法解方程 $\text{[math]}$ ，下列配方结果正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024九上·江油月考) 若点 $\text{[math]}$ ， $\text{[math]}$ 关于原点对称，则m、n的值为（）

A . $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024·旺苍模拟) 剪纸艺术是最古老的中国民间艺术之一，先后入选中国国家级非物质文化遗产名录和人类非物质文化遗产代表作名录．鱼与“余”同音，寓意生活富裕、年年有余，是剪纸艺术中很受喜爱的主题．以下关于鱼的剪纸中，是轴对称图形，但不是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2024·旺苍模拟) “文明丰都·幸福你我”，丰都正在积极创建全国文明城市．丰都宏运公司楼顶公益广告牌上“文明丰都”几个字是霓红灯，几个字一个接一个亮起来（亮后不熄灭）直至全部亮起来再循环，当路人一眼望去，能够看到几个字全在的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024九上·北川月考) 已知 $\text{[math]}$ 是二次函数，则 $\text{[math]}$ 的值为（）

A . 0 B . 1 C . －1 D . 1或－1

答案解析收藏纠错 + 选题
6. (2024·旺苍模拟) 如图，直线 $\text{[math]}$ 与x轴、y轴分别相交于 $\text{[math]}$ 、B两点， $\text{[math]}$ ，圆心 $\text{[math]}$ 的坐标为 $\text{[math]}$ ， $\text{[math]}$ 与y轴相切于原点O ，若将 $\text{[math]}$ 沿x轴向右移动，当 $\text{[math]}$ 与该直线相交时，横坐标为整数的点P的个数是（）

A . 2 B . 3 C . 4 D . 5

答案解析收藏纠错 + 选题
7. (2024·旺苍模拟) 关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 中，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则这个方程的根的情况是（）

A . 有两个相等的实数根 B . 没有实数根 C . 有一个正根和一个负根 D . 有两个正的实数根

答案解析收藏纠错 + 选题
8. (2024·旺苍模拟) 如图， $\text{[math]}$ 是 $\text{[math]}$ 的两条直径， $\text{[math]}$ 是劣弧 $\text{[math]}$ 的中点，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2024·瑞昌模拟) 如图1，矩形 $\text{[math]}$ 中，点E为 $\text{[math]}$ 的中点，点P沿 $\text{[math]}$ 从点B运动到点C ，设B ， P两点间的距离为x ， $\text{[math]}$ ，图2是点P运动时y随x变化的关系图象，则 $\text{[math]}$ 的长为（　　）

A . 6 B . 7 C . 8 D . 9

答案解析收藏纠错 + 选题
10. (2024·旺苍模拟) 如图，二次函数． $\text{[math]}$ 的图象经过点 $\text{[math]}$ ，且与 $\text{[math]}$ 轴交点的横坐标分别为 $\text{[math]}$ ，其中 $\text{[math]}$ ， $\text{[math]}$ ，下列结论：
① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ ；⑤ $\text{[math]}$ ；其中，结论正确的个数有（）

A . 2个 B . 3个 C . 4个 D . 5个

答案解析收藏纠错 + 选题

二、填空题（把正确答案直接写在答题卡对应题目的横线上，每小题4分，共24分）

11. (2024九下·河池模拟) “八月十五云遮月，正月十五雪打灯”是一句谚语，意思是说如果八月十五晚上阴天的话，正月十五晚上就下雪，你认为农谚说的是（填写“必然事件”或“不可能事件”或“随机事件”）．

答案解析收藏纠错 + 选题
12. (2024·旺苍模拟) 已知 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
13. (2024·旺苍模拟) 若点 $\text{[math]}$ ， $\text{[math]}$ 是二次函数 $\text{[math]}$ 图象上的两点，则 $\text{[math]}$ $\text{[math]}$ （填 $\text{[math]}$ ）．

答案解析收藏纠错 + 选题
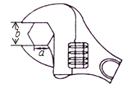
14. (2024·旺苍模拟)
如图，要拧开一个边长为a=12mm的六角形螺帽，扳手张开的开口b至少要 mm．

答案解析收藏纠错 + 选题
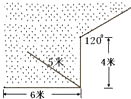
15. (2024·旺苍模拟) 如图，一根5m长的绳子，一端拴在围墙墙角的柱子上，另一端拴着一只小羊A（羊只能在草地上活动），那么小羊A在草地上的最大活动区域面积是平方米．

答案解析收藏纠错 + 选题
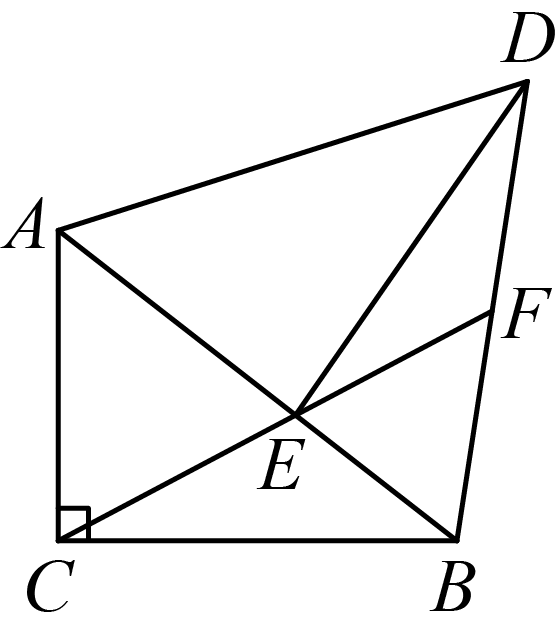
16. (2024·旺苍模拟) 如图，在△ABC中，∠ACB=90°，AC=3，BC=4，将△ABC绕点A旋转，使点C落在AB边上的点E处，点B落在点D处，连接BD，CE，延长CE交BD于点F，则EF的长为

答案解析收藏纠错 + 选题

三、解答题（要求写出必要的解答步骤或证明过程．共96分）

17. (2024·旺苍模拟) 选择适当的方法解方程；
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
18. (2024·旺苍模拟) 先化简，再求值 $\text{[math]}$ ，其中 $\text{[math]}$ 为方程 $\text{[math]}$ 的根．

答案解析收藏纠错 + 选题
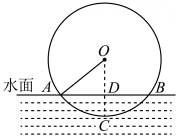
19. (2024·旺苍模拟) 唐代李皋发明了“桨轮船”，这种船是原始形态的轮船，是近代明轮航行模式之先导．如图，某桨轮船的轮子被水面截得的弦 $\text{[math]}$ 长8m，设圆心为 $\text{[math]}$ ， $\text{[math]}$ 交水面 $\text{[math]}$ 于点D ，轮子的吃水深度 $\text{[math]}$ 为2m，求该桨轮船的轮子直径．

答案解析收藏纠错 + 选题
20. (2024·旺苍模拟) 如图，在平面直角坐标系 $\text{[math]}$ xOy中，点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）以点C为旋转中心，把 $\text{[math]}$ 逆时针旋转 $\text{[math]}$ ，画出旋转后的 $\text{[math]}$ ；
2. （2）在（1）的条件下，
  ①点A经过的路径 $\text{[math]}$ 的长度为（结果保留 $\text{[math]}$ ）；
  ②连接 $\text{[math]}$ ，线段 $\text{[math]}$ 的中点的坐标为．
答案解析收藏纠错 + 选题
21. (2024·旺苍模拟) 关于x的方程 $\text{[math]}$ －(2k+1)x+ $\text{[math]}$ =0．
1. （1）求证：方程有两个不相等的实数根；
2. （2）已知等腰△ABC的一边长c=3，另两边长a、b恰是方程的两个根，求△ABC的周长．
答案解析收藏纠错 + 选题
22. (2024·旺苍模拟) 后屯农户收获杏时，有农户种杏树44株，现进入第三年收获。收获时，先随机采摘5株果树上的杏，称得每株果树上杏重量如下（单位：kg）：35，35，34，39，37。
1. （1）试估计这一年该农户杏的总产量约是多少？
2. （2）若市场上每千克杏售价5元，则该农户这一年卖杏的收入为多少？
3. （3）已知该农户第一年果树收入5500元，根据以上估算第二年、第三年卖杏收入的年平均增长率。
答案解析收藏纠错 + 选题
23. (2024·长沙模拟) 高尔基说：“书，是人类进步的阶梯．”阅读可以启智增慧，拓展视野．为了解学生寒假阅读情况，开学初学校进行了问卷调查，并对部分学生假期（28天）的阅读总时间作了随机抽样分析．设被抽样的每位同学寒假阅读的总时间为t（小时），阅读总时间分为四个类别：A（0≤t＜12），B（12≤t＜24），C（24≤t＜36），D（t≥36），将分类结果制成两幅统计图（尚不完整）．
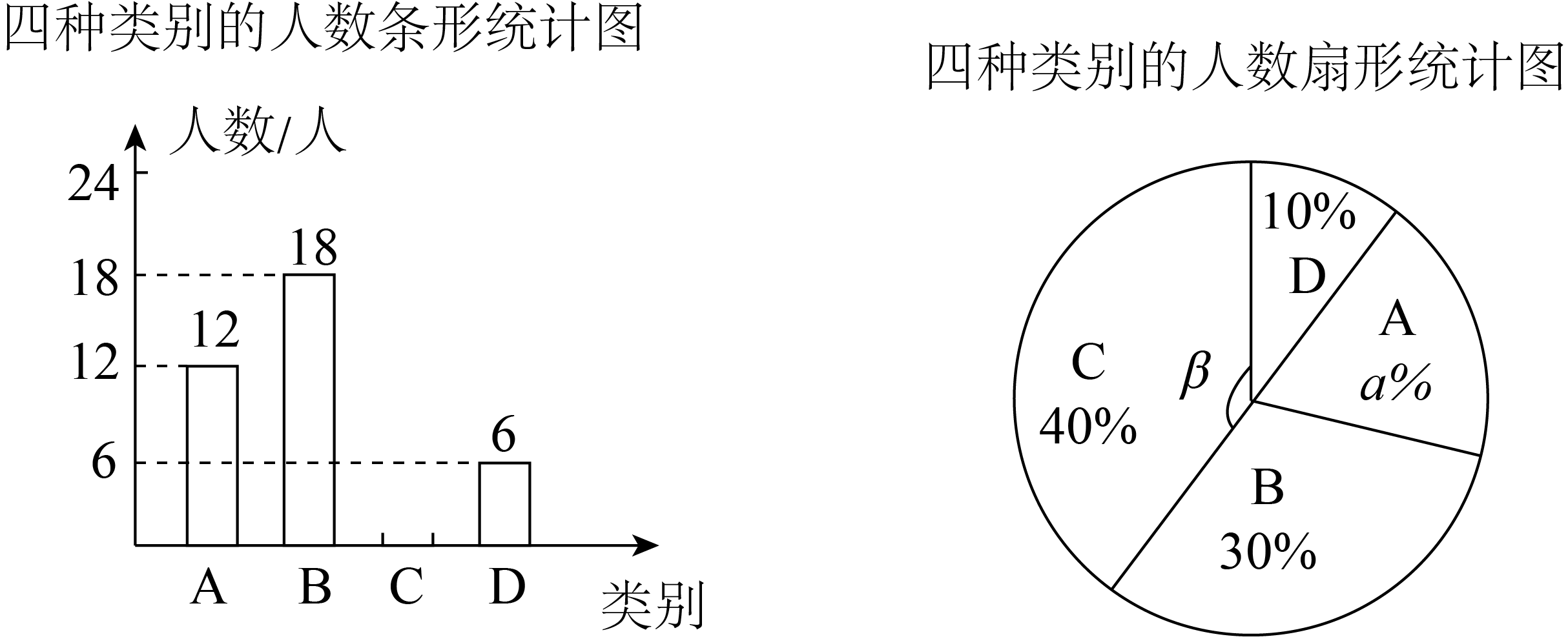
根据以上信息，回答下列问题：
1. （1）本次抽样的样本容量为，请补全条形统计图；
2. （2）扇形统计图中a的值为，圆心角β的度数为；
3. （3）若该校有2000名学生，估计寒假阅读的总时间少于24小时的学生有多少名？
4. （4）政教处决定从本次调查阅读时长前四名学生甲、乙、丙、丁中，随机抽取2名同学参加该校“阅读之星”竞选，请用树状图或列表法求恰好选中甲和乙的概率．
答案解析收藏纠错 + 选题
24. (2024·旺苍模拟) 我市某企业安排20名工人生产甲、乙两种产品，根据生产经验，每人每天生产2件甲产品或1件乙产品（每人每天只能生产一种产品）．甲产品生产成本为每件10元；若安排1人生产一件乙产品，则成本为38元，以后每增加1人，平均每件乙产品成本降低2元．规定甲产品每天至少生产20件．设每天安排 $\text{[math]}$ 人生产乙产品．
1. （1）根据信息填表：
  产品种类
  每天工人数（人）
  每天产量（件）
  每件产品生产成本（元）
  甲
  
  10
  乙
  
  $\text{[math]}$
  $\text{[math]}$
2. （2）为了增加利润，企业须降低成本，该企业如何安排工人生产才能使得每天的生产总成本最低？最低成本是多少？
答案解析收藏纠错 + 选题
25. (2024·旺苍模拟) 如图，等腰直角 $\text{[math]}$ 与 $\text{[math]}$ 交于点B ， C ， $\text{[math]}$ ，延长 $\text{[math]}$ 与 $\text{[math]}$ 分别交于点D ， E ，连接 $\text{[math]}$ ，并延长 $\text{[math]}$ 至点F ，使得 $\text{[math]}$ ．
1. （1）求 $\text{[math]}$ 的度数；
2. （2）求证： $\text{[math]}$ 与 $\text{[math]}$ 相切；
3. （3）若 $\text{[math]}$ 的半径为2，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
26. (2024·旺苍模拟) 如图，二次函数 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 时的函数值相等，其图象与x轴交于A、B两点，与y轴正半轴交于C点．
1. （1）求二次函数的解析式．
2. （2）在第一象限的抛物线上求点P ，使得 $\text{[math]}$ 最大．
3. （3）点Q是抛物线上x轴上方一点，若 $\text{[math]}$ ，求Q点坐标．
答案解析收藏纠错 + 选题