吉林省长春市重点学校2023-2024学年高三上学期数学期中...

更新时间：2023-12-29 浏览次数：32 类型：期中考试

一、单选题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项一项是符合题目要求的.

1. (2023高三上·长春期中) 已知集合 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 中元素的个数为（）

A . 3 B . 4 C . 5 D . 6

答案解析收藏纠错 + 选题
2. (2023高三上·长春期中) 已知复数 $\text{[math]}$ 满足 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023高三上·长春期中) 在 $\text{[math]}$ 中， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 2

答案解析收藏纠错 + 选题
4. (2023高三上·长春期中) 已知椭圆 $\text{[math]}$ 的一个焦点与抛物线 $\text{[math]}$ 的焦点重合，长轴长等于圆 $\text{[math]}$ 的半径，则椭圆 $\text{[math]}$ 的方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023高三上·长春期中) 已知函数 $\text{[math]}$ 在区间 $\text{[math]}$ 上单调递减，则 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023高三上·长春期中) 直线 $\text{[math]}$ 圆 $\text{[math]}$ 相交于 $\text{[math]}$ ， $\text{[math]}$ 两点，则“ $\text{[math]}$ ”是“ $\text{[math]}$ ”的（）

A . 充分而不必要条件 B . 必要而不充分条件 C . 充分必要条件 D . 既不充分又不必要条件

答案解析收藏纠错 + 选题
7. (2023高三上·长春期中) 设 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023高三上·长春期中) 已知 $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、多选题：本题共4小题，每小题5分,共20分.在每小题给出的四个选项中，至少有两项是符合题目要求的.选对得5分，少选得2分，多选或错选得0分.

9. (2023高三上·长春期中) 下列说法正确的是（）

A . 一组数1，5，6，7，10，13，15，16，18，20的第75百分位数为16 B . 在经验回归方程 $\text{[math]}$ 中，当解释变量 $\text{[math]}$ 每增加1个单位时，相应变量 $\text{[math]}$ 增加 $\text{[math]}$ 个单位 C . 数据 $\text{[math]}$ 的方差为 $\text{[math]}$ ，则数据 $\text{[math]}$ 的方差为 $\text{[math]}$ D . 一个样本的方差 $\text{[math]}$ ，则这组样本数据的总和等于100

答案解析收藏纠错 + 选题
10. (2023高三上·长春期中) 已知函数 $\text{[math]}$ 的图象为C ，以下说法中正确的是（）

A . 函数 $\text{[math]}$ 的最大值为 $\text{[math]}$ B . 图象C关于 $\text{[math]}$ 中心对称 C . 函数 $\text{[math]}$ 在区间 $\text{[math]}$ 内是增函数 D . 函数 $\text{[math]}$ 图象上，横坐标伸长到原来的2倍，向左平移 $\text{[math]}$ 可得到 $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2023高三上·长春期中) 在直三棱柱 $\text{[math]}$ 中，底面 $\text{[math]}$ 为等腰直角三角形，且满足 $\text{[math]}$ ，点 $\text{[math]}$ 满足 $\text{[math]}$ ，其中 $\text{[math]}$ ， $\text{[math]}$ ，则下列说法正确的是（）

A . 当 $\text{[math]}$ 时， $\text{[math]}$ 的面积 $\text{[math]}$ 的最大值为 $\text{[math]}$ B . 当 $\text{[math]}$ 时，三棱锥 $\text{[math]}$ 的体积为定值 C . 当 $\text{[math]}$ 时，有且仅有一个点 $\text{[math]}$ ，使得 $\text{[math]}$ D . 当 $\text{[math]}$ 时，存在点 $\text{[math]}$ ，使得 $\text{[math]}$ 平面 $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2023高三上·长春期中) 已知定义域为 $\text{[math]}$ 的函数 $\text{[math]}$ 对任意实数 $\text{[math]}$ 都有 $\text{[math]}$ ，且 $\text{[math]}$ ，则以下结论正确的有（）

A . $\text{[math]}$ B . $\text{[math]}$ 是偶函数 C . $\text{[math]}$ 关于 $\text{[math]}$ 中心对称 D . $\text{[math]}$

答案解析收藏纠错 + 选题

三、填空题：本题共4小题，每小题5分,共20分.

13. (2023高三上·长春期中) $\text{[math]}$ 的展开式中含 $\text{[math]}$ 项的系数为.

答案解析收藏纠错 + 选题
14. (2023高三上·长春期中) 已知数列 $\text{[math]}$ 的前n项和为 $\text{[math]}$ ，则 $\text{[math]}$ =.

答案解析收藏纠错 + 选题
15. (2023高三上·长春期中) 已知双曲线 $\text{[math]}$ 的左､右焦点分别为 $\text{[math]}$ ，过双曲线 $\text{[math]}$ 上一点 $\text{[math]}$ 向 $\text{[math]}$ 轴作垂线，垂足为 $\text{[math]}$ ，若 $\text{[math]}$ 且 $\text{[math]}$ 与 $\text{[math]}$ 垂直，则双曲线 $\text{[math]}$ 的离心率为.

答案解析收藏纠错 + 选题
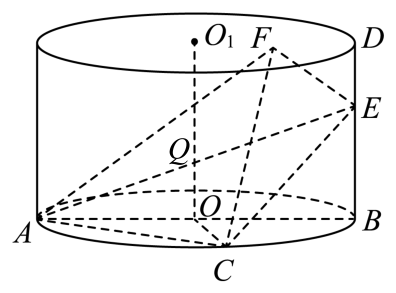
16. (2023高三上·长春期中) 如图，圆柱 $\text{[math]}$ 的底面半径和母线长均为3， $\text{[math]}$ 是底面直径，点 $\text{[math]}$ 在圆 $\text{[math]}$ 上且 $\text{[math]}$ ，点 $\text{[math]}$ 在母线 $\text{[math]}$ 上， $\text{[math]}$ ，点 $\text{[math]}$ 是上底面的一个动点，且 $\text{[math]}$ ，则四面体 $\text{[math]}$ 的外接球的体积为.

答案解析收藏纠错 + 选题

四、解答题：17题10分，18-22题每题12分，共70分.

17. (2023高三上·长春期中) 已知数列 $\text{[math]}$ 的前 $\text{[math]}$ 项的和为 $\text{[math]}$ ，且 $\text{[math]}$ .
1. （1）求数列 $\text{[math]}$ 的通项公式；
2. （2）设 $\text{[math]}$ ，求数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和 $\text{[math]}$ .
答案解析收藏纠错 + 选题
18. (2023高三上·长春期中) 在 $\text{[math]}$ 中，内角 $\text{[math]}$ . $\text{[math]}$ . $\text{[math]}$ 的对边分别为 $\text{[math]}$ ，且 $\text{[math]}$ ．
1. （1）求角 $\text{[math]}$ 的大小；
2. （2）若点 $\text{[math]}$ 满足 $\text{[math]}$ ，且 $\text{[math]}$ ，求 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
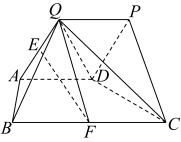
19. (2023高三上·长春期中) 已知多面体 $\text{[math]}$ ，四边形 $\text{[math]}$ 是等腰梯形， $\text{[math]}$ ， $\text{[math]}$ ，四边形 $\text{[math]}$ 是菱形， $\text{[math]}$ ， E ， F分别为QA ， BC的中点， $\text{[math]}$ .
1. （1）求证：平面 $\text{[math]}$ 平面 $\text{[math]}$ ；
2. （2）求点 $\text{[math]}$ 到平面 $\text{[math]}$ 的距离.
答案解析收藏纠错 + 选题
20. (2023高三上·长春期中) 甲、乙两人进行“抗击新冠疫情”知识竞赛，比赛采取五局三胜制，约定先胜三局者获胜，比赛结束．假设在每局比赛中，甲获胜的概率为 $\text{[math]}$ ，乙获胜的概率为 $\text{[math]}$ ，各局比赛相互独立．
1. （1）求甲获胜的概率；
2. （2）设比赛结束时甲和乙共进行了 $\text{[math]}$ 局比赛，求随机变量 $\text{[math]}$ 的分布列及数学期望．
答案解析收藏纠错 + 选题
21. (2023高三上·长春期中) 已知椭圆 $\text{[math]}$ 的离心率为 $\text{[math]}$ ，且点 $\text{[math]}$ 在椭圆 $\text{[math]}$ 上．
1. （1）求椭圆 $\text{[math]}$ 的标准方程；
2. （2）若直线 $\text{[math]}$ 交椭圆 $\text{[math]}$ 于 $\text{[math]}$ 两点，线段 $\text{[math]}$ 的中点为 $\text{[math]}$ ， $\text{[math]}$ 为坐标原点，且 $\text{[math]}$ ，求 $\text{[math]}$ 面积的最大值．
答案解析收藏纠错 + 选题
22. (2023高三上·长春期中) 已知函数 $\text{[math]}$ ，其中a为实数.
1. （1）当 $\text{[math]}$ 时，求曲线 $\text{[math]}$ 在点 $\text{[math]}$ 处的切线方程；
2. （2）是否存在实数a，使得 $\text{[math]}$ 恒成立？若不存在，请说明理由，若存在，求出a的值并加以证明.
答案解析收藏纠错 + 选题