吉林省松原市前郭县第三中学2023-2024学年八年级上学期...

更新时间：2024-03-21 浏览次数：27 类型：期中考试

一、单项选择题（每小题2分，共12分）

1. (2023八上·船营期中) 图示是我国几家银行的标志，其中不是轴对称图形的是（）

A . 中国银行 B . 中国人民银行 C . 中国工商银行 D . 中国建设银行

答案解析收藏纠错 + 选题
2. (2023八上·松原期中) 如图，为估计池塘岸边A，B的距离，小杰在池塘的一侧选取一点O，测得OA=10米，OB=6米，A，B间的距离可能是（）

A . 4米 B . 12米 C . 16米 D . 22米

答案解析收藏纠错 + 选题
3. (2023八上·松原期中) 老师上课用磁力小棒设计了一个平分角的仪器，用它可以平分一个已知角，其中AB=AD，BC=DC，将点A放在一个角的顶点，AB和AD沿着这个角的两边放下，利用全等三角形的性质就能说明射线AC是这个角的平分线．这里判定△ABC和△ADC是全等三角形的依据是（）

A . SSS B . ASA C . SAS D . AAS

答案解析收藏纠错 + 选题
4. (2023八上·松原期中) 如图，将透明直尺叠放在正五边形微章ABCDE上，若直尺的下沿MN⊥DE于点O，且经过点B，上沿PQ经过点E，则∠ABM的度数为（）

A . 152° B . 126° C . 120° D . 108°

答案解析收藏纠错 + 选题
5. (2023八上·松原期中) 如图，BD是等边△ABC的边AC上的高，以点D为圆心，DB长为半径作弧交BC的延长线于点E，则∠DEC=（）

A . 20° B . 25 C . 30° D . 35°

答案解析收藏纠错 + 选题
6. (2024八上·番禺期末) 如图，在正方形网格中有M，N两点，在直线 $\text{[math]}$ 上求一点P使PM＋PN最短，则点P应选在（）

A . A点 B . B点 C . C点 D . D点

答案解析收藏纠错 + 选题

二、填空题（每小题3分，共24分）

7. (2023八上·吉林期中) 如图，在△ABC中，D是BC延长线上一点，∠B=40°，∠ACD=120°，则∠A=°．

答案解析收藏纠错 + 选题
8. (2024·娄底模拟) 点M（3，-4）关于x轴的对称点的坐标是

答案解析收藏纠错 + 选题
9. (2023八上·松原期中) 如图①所示是中国古塔，图②所示的正八边形是塔基的平面示意图，则该正八边形内角和的度数为

答案解析收藏纠错 + 选题
10. (2023八上·松原期中) 等腰三角形有一个角是94°，则它一个底角的度数为

答案解析收藏纠错 + 选题
11. (2023八上·船营期中) 如图，∠D=∠C=90°，请你再添加一个条件，使△ABD≌△ABC，你添加的条件是

答案解析收藏纠错 + 选题
12. (2023八上·船营期中) 如图，△ABC中，∠B=60°，∠C=56°，点D为BC边上一动点。分别作点D关于AB，AC的对称点E，F，连接AE，AF．则∠EAF的度数等于

答案解析收藏纠错 + 选题
13. (2023八上·松原期中) 如图，平面内不共线三点A，B，C，操作如下：

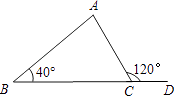
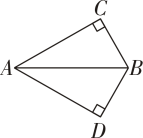
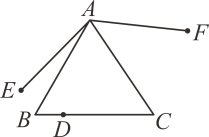
（1）连接BC，以点B为圆心，以CB的长为半径画弧；（2）连接AC，以点A为圆心，以AC的长为半径画弧，两弧相交于点D；（3）连接CD，且过A，B作直线，则A，B一定在线段CD的垂直平分线上，依据是：

答案解析收藏纠错 + 选题
14. (2023八上·船营期中) 如图，在Rt△ABC中，∠C=90°，BC<AC．点D，E分别在边AB，BC上，连接DE，将△BDE沿DE折叠，点B的对应点为点B'，若点B'刚好落在边AC上，∠CB'E=30°，CE=3，则BC的长为

答案解析收藏纠错 + 选题

三、解答题（每小题5分，共20分）

15. (2023八上·船营期中) 如图， $\text{[math]}$ ，直线 $\text{[math]}$ 与 $\text{[math]}$ 分别交于点E ， F ， $\text{[math]}$ 上有一点G且 $\text{[math]}$ ， $\text{[math]}$ ．求 $\text{[math]}$ 的度数．

答案解析收藏纠错 + 选题
16. (2023八上·船营期中) 如图，点A，B，C，D在同一直线上， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．求证： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
17. (2023八上·松原期中) 如图，已知∠B=∠C，AB∥DE，DE交BC于点E．求证：△DEC是等腰三角形．

答案解析收藏纠错 + 选题
18. (2023八上·船营期中) 如图是由三个小正方形组成的图案，请在图中补画一个小正方形，使补画后的图案是轴对称图形．请用两种不同方法补画图形，并画出各自的对称轴．

答案解析收藏纠错 + 选题

四、解答题（每小题7分，共28分}

19. (2023八上·松原期中) 如图，在边长为1个单位长度的小正方形网格中，给出了△ABC（顶点是网格线的交点）
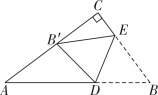
和直线l．
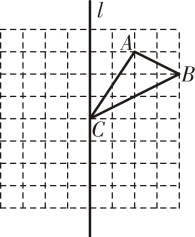
⑴在直线l上找一点P，使点P到边AB， BC的距离相等；
⑵画出△ABC关于直线l对称的图形△A₁B₁C₁；再将△A₁B₁C₁向下平移4个单位长度，画出平移后得到的图形△A₂B₂C₂；
⑶结合轴对称变换和平移变换的有关性质，两个对应图形△ABC和△A₂B₂C₂的对应点所具有的性质是
A.对应点连线互相平行．
B.对应点连线被直线l垂直平分．
C.对应点连线被直线l平分或与直线l重合．

答案解析收藏纠错 + 选题
20. (2023八上·松原期中) 如图，AD是△ABC的角平分线，且DE⊥AB，∠B=50°，∠C=60°．
1. （1）求∠ADC的度数；
2. （2）若DE=8，点F是AC上的动点，求DF的最小值．
答案解析收藏纠错 + 选题
21. (2023八上·武清期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 边的垂直平分线分别交 $\text{[math]}$ 、 $\text{[math]}$ 于点 $\text{[math]}$ 、 $\text{[math]}$ ，连接 $\text{[math]}$ ，作 $\text{[math]}$ 于点 $\text{[math]}$ ，且 $\text{[math]}$ 为 $\text{[math]}$ 的中点．
1. （1）试说明： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数．
答案解析收藏纠错 + 选题
22. (2023八上·船营期中) 在△ABC和△ADE中，AB=AD，AC=AE，∠BAC=∠DAE．
1. （1）如图①，求证：∠ABC=∠ADE；
2. （2）如图②，若AD平分∠CAE，∠DAE=30°，点C在线段BE上，则∠D=度．
答案解析收藏纠错 + 选题

五、解答题（每小题8分，共16分）

23. (2023八上·船营期中) 如图，已知点D、E是△ABC内两点，且∠BAE＝∠CAD，AB＝AC，AD＝AE.
1. （1）求证： $\text{[math]}$ .
2. （2）延长BD、CE交于点F，若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的度数.
答案解析收藏纠错 + 选题
24. (2023八上·船营期中) 如图，在△ABC中，∠ACB=90°，点E，F在边AB上，将边AC沿CE翻折，使点A落在AB上的点D处，再将边BC沿CF翻折，使点B落在CD的延长线上的点B'处，
1. （1）求∠ECF的度数；
2. （2）若CE=4，B'F=1，求△BCE的面积．
答案解析收藏纠错 + 选题

六、解答题（每小题10分，共20分）

25. (2023八上·船营期中) 如图，AE与BD交于点C，AC=EC，BC=DC，AB=6cm，点P从A出发，沿A→B→A的方向以3 cm/s的速度运动；点Q从D出发，沿D→E的方向以1 cm/s的速度运动．点P，Q同时出发，当点P到达A时，P，Q两点同时停止运动，设点P的运动时间为t（s）．
1. （1）直接写出线段BP的长；（用含t的式子表示）
2. （2）求DE的长；
3. （3）连接PQ，当线段PQ经过点C时，直接写出t的值．
答案解析收藏纠错 + 选题
26. (2023八上·船营期中) △ABC中，AB=AC，点D为射线BC上一个动点（不与B，C重合），以AD为一边向AD的左侧作△ADE，使AD=AE，∠DAE=∠BAC，过点E作BC的平行线，交直线AB于点F，连接BE．
1. （1）如图①，若∠BAC=∠DAE=60°，则△BEF是三角形；
2. （2）若∠BAC=∠DAE≠60°
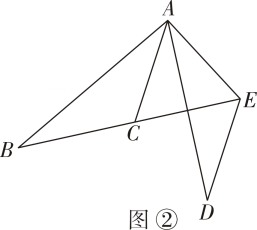
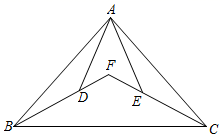
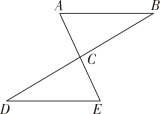
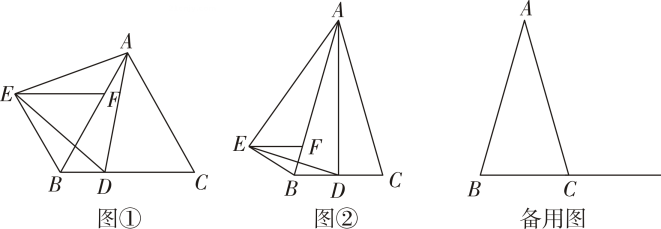
  ①如图②，当点D在线段BC上移动，判断△BEF的形状并证明；
  ②当点D在线段BC的延长线上移动，△BEF是什么三角形？请直接写出结论并画出相应的图形．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

吉林省松原市前郭县第三中学2023-2024学年八年级上学期...

副标题：

*注意事项：

吉林省松原市前郭县第三中学2023-2024学年八年级上学期...

试题分析

总体分析

题量分析

难度分析

知识点分析