吉林省长春市新解放学校初中部2023-2024学年九年级上学...

更新时间：2024-03-19 浏览次数：18 类型：期中考试

一、选择题（共8小题，每小题3分，共24分）

1. (2023九上·长春期中) 有4筐草莓，以每筐2千克为标准，超过的千克数记为正数，不足的千克数记为负数。记录如下：-0.1，-0.3，+0.2．+0.3．则这4筐草莓中，质量最大的是（）

A . 1.9千克 B . 1.7千克 C . 2.2千克 D . 2.3千克

答案解析收藏纠错 + 选题
2. (2023九上·长春期中) 上半年长春的经济增长表现十分出色，位居全国城市前列．GDP约为336 000 000 000元，增长9.1%．数据336 000 000 000用科学记数法表示为（）

A . 3.36×10⁹ B . 33.6×10¹⁰ C . 3.36×10¹¹ D . 3.36×10¹²

答案解析收藏纠错 + 选题
3. (2023九上·长春期中) 下列运算正确的是（）

A . a³+a²=a⁵ B . a³·a²=a⁵ C . （a³）²=a⁵ D . a⁶÷a²=a³

答案解析收藏纠错 + 选题
4. (2023九上·长春期中) 下列生活中的实例，可以用基本事实：“两点之间线段最短”解释的是（）

A . 小狗看到远处的食物，总会径直奔向食物． B . 从一条河道能向集镇引一条最短的水渠． C . 把一根木条固定到墙上至少需要两颗钉子． D . 经过刨平的木板上的两个点，能弹出一笔直的墨线。

答案解析收藏纠错 + 选题
5. (2023九上·长春期中) 如图是一个小正方体的展开图，把展开图折叠成小正方体后，“建”字对面的字是（）

A . 和 B . 谐 C . 社 D . 会

答案解析收藏纠错 + 选题
6. (2023九上·长春期中) 如图，小明想要测量学校操场上旗杆AB的高度，他作了如下操作：

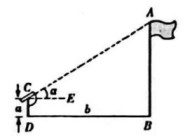
（1）在点C处放置测角仪，测得旗杆顶的仰角∠ACE=α；（2）量得测角仪的高度CD=a；（3）量得测角仪到旗杆的水平距离DB=b．利用解直角三角形的知识，旗杆的高度为（）

A . a+ btanα B . a+ $\text{[math]}$ C . a+bsinα D . a+ $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023九上·长春期中) 如图，在△ABC中，AC>BC，∠ACB为钝角．按下列步骤作图：①以点B为圆心，适当长为半径作圆弧，交BC于点D，交AB于点E；②以点C为圆心，BD长为半径作圆弧，交AC于点F：③以点F为圆心，DE长为半径作圆弧，交②中所作的圆弧于点G；④作射线CG交AB于点H．下列说法不正确的是（）

A . ∠ACH=∠B B . ∠AHC=∠ACB C . ∠CHB=∠A+∠B D . ∠CHB=∠HCB

答案解析收藏纠错 + 选题
8. (2023九上·长春期中) 如图，已知A（0，3）， B（1，0）．以线段AB为边，在第一象限内作正方形ABCD．点C落在函数y= $\text{[math]}$ （x>0）的图象上，将正方形ABCD沿x轴负方向平移a个单位长度，使点D恰好落在函数y= $\text{[math]}$ （x>0）的图象上的点D'处，则a的值为（）

A . 1 B . $\text{[math]}$ C . 2 D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（共6小题，每小题3分，共18分）

9. (2023九上·长春期中) 分解因式：a²b-ab=

答案解析收藏纠错 + 选题
10. (2023九上·长春期中) 关于x的方程x²-4x+c=0有两个不相等的实数，则实数c的取值范围是

答案解析收藏纠错 + 选题
11. (2023九上·长春期中) 某种水果的售价为每千克a元，用面值为50元的人民币购买了3千克这种水果，应找回元（用含a的代数式表示）．

答案解析收藏纠错 + 选题
12. (2023九上·长春期中) 如图，在平面直角坐标系中，A、B两点的坐标分别为A（-1，2）、B（0，2）， C、D两点的坐标分别为C（0，-1）、D（2，-1）．若线段AB和线段CD是位似图形，且位似中心在y轴上，则位似中心的坐标为

答案解析收藏纠错 + 选题
13. (2023九上·长春期中) 如图，AB是⊙O的直径，BC是⊙O的弦。BC= 3，将 $\text{[math]}$ 沿着BC折叠后恰好经过点O，则AB的长为

答案解析收藏纠错 + 选题
14. (2023九上·长春期中) 如图，已知一抛物线形大门，其地面宽度AB=18米，一位同学站在门内，在离门脚B点1米远的D处，垂直地面立，起一根1.7米长的木杆．其顶端恰好顶在抛物线形门上C处。则该大门的高h为米．

答案解析收藏纠错 + 选题

三、解答题（共10小题，共78分）

15. (2023九上·长春期中) 先化简，再求值：（2+a）（2-a）+a（a+1），其中a=-6．

答案解析收藏纠错 + 选题
16. (2023九上·长春期中) 长春地铁的不断完善给广大人民的出行带来了很大的变化，不仅给人们带来了快捷、便利、有序的交通和良好的乘车环境，还让人们更多地感受到生活质量的提高和享受．长春地铁2号线某地铁入口检票处有A、B两个闸口，假设每名乘客可随机选择一个闸口通过．当甲、乙、丙三名乘客先后通过该入口检票处时，请用画树状围的方法求出三名乘客选择同一闸口通过的概率．

答案解析收藏纠错 + 选题
17. (2023九上·长春期中) 甲、乙两同学的家与某科技馆的距离均为5000米．甲，乙两人同时从家出发去科技馆，甲同学先步行600米，然后乘公交车，乙同学骑自行车．已知乙骑自行车的速度是甲步行速度的4倍，公交车的速度是乙骑自行车速度的2倍，结果甲同学比乙同学早到2分钟．求甲到达科技馆时，乙离科技馆还有多远？

答案解析收藏纠错 + 选题
18. (2023九上·长春期中) 如图，已知矩形ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F．
1. （1）求证：四边形AFCE是菱形；
2. （2）当BC= $\text{[math]}$ AB时，菱形AFCE的面积与矩形ABCD的面积比为
答案解析收藏纠错 + 选题
19. (2023九上·长春期中) 据吉林省2022年国民经济和社会发展公报，2022年末全省快递业务量58194.02万件，下降6.4%，快递业务收入71.38亿元，下降7.2%．根据公报的数据绘制了2018年-2022年全省快递业务量及其增长速度的统计图表，根据该统计图表解答下列问题：
2018- 2022年快递业务量及其增长速度
1. （1）吉林省从2018年到2022年，全省快递业务量最多年份比最少年份多万件：
2. （2）吉林省从2018年到2022年，全省快递业务量增长速度的中位数是%：
3. （3）与2020年相比，2021年吉林省快递业务量增加了万件，快递业务量增长速度降低了百分点（注：1%为1个百分点）：
4. （4）根据统计图提供的信息，有下列说法，其中正确的是____（填写字母）．
  
  A . 从2018年到2021年，全省快递业务量持续增长． B . 2021 年快递业务收入为71.38÷（1-7.2%）≈76.92（亿元）． C . 从2020年到2022年，全省快递业务量增长速度持续下降，因此这三年快递业务量增长率均为负增长．
答案解析收藏纠错 + 选题
20. (2023九上·长春期中) 图①、图②、图③均是6×5的正方形网格，每个小正方形的边长均为1，每个小正方形的顶点称为格点。点A、B、M、N均在格点上，只用无刻度的直尺，分别在给定的网格中按要求作图．
1. （1）在图①中，找一格点C，连接AC，使∠BAC=45°；
2. （2）在图②中，在线段MV上找一点C，连接AC，使∠BAC= 45°：
3. （3）在图③中，经过点A、B、M作圆，在劣弧 $\text{[math]}$ 上找一点C，连接AC，使∠BAC=45°．
答案解析收藏纠错 + 选题
21. (2023九上·长春期中) 甲、乙两台机器共同加工一批零件，一共用了6小时，在加工过程中乙机器因故障停止工作，排除故障后，乙机器提高了工作效率且保持不变，继续加工，甲机器在加工过程中工作效率保持不变，甲、乙两台机器加工零件的总数y（个）与甲加工时间x（时）之间的函数图象为折线OA-AB-BC．如图所示．
1. （1）这批零件一共有个，甲机器每小时加工个零件；
2. （2）在乙提高工作效率后，求y与x之间的函数解析式：
3. （3）乙机器排除故障后，直接写出甲加工多长时间时，甲与乙加工的零件个数相差10个．
答案解析收藏纠错 + 选题
22. (2023九上·长春期中) 有关阿基米德折弦定理的探讨与应用
1. （1） [问题呈现]
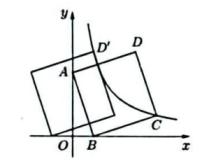
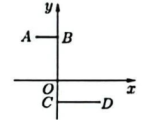
  阿基米德折弦定理：如图①，AB和BC是⊙O的两条弦（即折线AB-BC是圆的一条折弦），BC> AB，点M是 $\text{[math]}$ 的中点，则从点M向BC作垂线，垂足D是折弦ABC的中点，即CD=DB+BA．
  下面是运用“截长法”证明CD=DB+BA的部分证明过程.
  证明：如图②，在CD上截取CE=AB，连接MA、MB、MC和ME.
  ∵M是 $\text{[math]}$ 的中点，∴MA=MC.
  ……
  请按照上面的证明思路，写出该证明的剩余部分.
2. （2） [理解运用]
  如图③，△ABC内接于⊙O，过点O作OD⊥AB于点D，延长DO交⊙O于点E，过点E作EF⊥AC于点F.若AC=10，BC=4，则CF的长为
3. （3） [实践应用]
  如图④，等边△ABC内接于⊙O，点D是 $\text{[math]}$ 上一点，且∠ABD= 45°，连接CD.若AB=2，则△BDC的周长为
答案解析收藏纠错 + 选题
23. (2023九上·长春期中) 如图， $\text{[math]}$ ABCD中，AB=AC=6，BC=4，点O是AC的中点。动点P从点A出发沿折线AB- BC以每秒2个单位长度向终点C运动，连接OP，作点A关于直线OP的对称点A'，连接PA'、OA'．设点P运动的时间为t秒．
1. （1） $\text{[math]}$ ABCD的面积为
2. （2）用含t的代数式表示线段BP的长：
3. （3）当OA'∥BC时，求t的值：
4. （4）当点A'在 $\text{[math]}$ ABCD的内部时，直接写出t的取值范围．
答案解析收藏纠错 + 选题
24. (2023九上·长春期中) 在平面直角坐标系中，点O为坐标原点，抛物线y=x²+bx-2（b是常数）经过点（3，1）．点A的坐标为（-mn，0），点B在该抛物线上，横坐标为1+m．其中m>0．
1. （1）求该抛物线对应的函数表达式及顶点坐标；
2. （2）当点B到两坐标轴的距离相等时，求点A的坐标；
3. （3）该抛物线与x轴的左交点为P，当抛物线在点P和点B之间的部分（包括P、B两点）的最高点与最低点的纵坐标之差为2m+1时，求m的值；
4. （4）当点B在x轴下方时，过点B作BC⊥y轴于点C，连接AC、BO．若四边形AOBC的边和抛物线有两个交点（不包括四边形AOBC的顶点），设这两个交点分别为点E、点F，线段BO的中点为D．当以点C、E、O、D（或以点C、F、O、D）为顶点的四边形的面积是四边形AOBC面积的一半时，直接写出所有满足条件的m的值．
答案解析收藏纠错 + 选题