浙江省台州市临海市第六教研区2023-2024学年八年级上学...

更新时间：2024-02-26 浏览次数：45 类型：期中考试

一、选择题（本大题共10小题，每小题3分，共30分．请选出各题中一个符合题意的正确选项，不选、多选、错选，均不给分）

1. (2023八上·临海期中) 第19届亚运会于2023年9月在杭州举行，下列历届亚运会会徽是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2024七下·宝安期中) 在△ABC中，作出AC边上的高，正确的是（）.

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2023八上·临海期中) 我校某班级计划在学校耕读园里搭三角形围栏，可以选择以下三种长度的木条组合的是（）

A . 3、4、8 B . 4、4、8 C . 3、5、6 D . 5、6、11

答案解析收藏纠错 + 选题
4. (2023八上·临海期中) 下图中显示的是从镜子中看到的背后墙上电子钟的读数，由此你可以推断这时的实际时间是（）

A . 10：05 B . 20：01 C . 20：10 D . 10：02

答案解析收藏纠错 + 选题
5. (2023八上·临海期中) 用直尺和圆规作一个角等于已知角，如图所示，能得出△OCD≌△O'C'D'的依据是（）

A . SSS B . SAS C . ASA D . AAS

答案解析收藏纠错 + 选题
6. (2023八上·临海期中) 等腰三角形的周长是8cm，其中一边长为2cm，则该等腰三角形的底边长为（）

A . 2cm B . 3cm C . 4cm D . 2cm或4cm

答案解析收藏纠错 + 选题
7. (2023八上·临海期中) 如图所示，△ABC与△DEF关于直线l对称，下列说法错误的是（）

A . AB＝DE B . ∠BAC＝∠EDF C . 点B和点E到直线l的距离相等 D . AC//DE

答案解析收藏纠错 + 选题
8. (2023八上·临海期中) 如图1是一个平板电脑支架，由托板、支撑板和底座构成，平板电脑放置在托板上，图2是其侧面结构示意图．现量得托板长AB＝10cm，支撑板顶端的C恰好是托板AB的中点，托板AB可绕点C转动，支撑板CD可绕点D转动．当CD⊥AB ，且射线DB恰好是∠CDE的平分线时，此时点B到直线DE的距离是（）

A . 5cm B . 6cm C . 8cm D . 10cm

答案解析收藏纠错 + 选题
9. (2023·云安模拟) 如图，点A ， B是4×4网格中的格点，网格中的每个小正方形的边长为1，如果以A ， B ， C为顶点的三角形是等腰三角形，则满足条件的所有格点C有（）个．

A . 6 B . 7 C . 8 D . 9

答案解析收藏纠错 + 选题
10. (2023八上·临海期中) 如图，将一张三角形纸片ABC的一角折叠，使点A落在△ABC外的A'处，折痕为DE ．如果∠A=α，∠DEA=β，∠CEA'=γ，∠BDA'=θ，那么下列式子中不一定成立的是（）

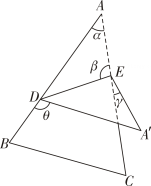
A . θ=2α+γ B . θ=180°﹣α﹣γ C . β= $\text{[math]}$ D . θ=2α+2β﹣180°

答案解析收藏纠错 + 选题

二、填空题（本题共6小题，每小题4分，共24分）

11. (2023八上·临海期中) 某校拍摄秋季运动会比赛盛况的摄影机架是三角形，这是利用了．

答案解析收藏纠错 + 选题
12. (2023八上·临海期中) 点（2023，-2024）关于x轴对称的点的坐标为．

答案解析收藏纠错 + 选题
13. (2023八上·临海期中) 如图，要测量池塘两岸相对的两点A ， B的距离，可以在池塘外取AB的垂线BF上的两点C ， D ，使BC＝CD ，再画出BF的垂线DE ，使E与A ， C在一条直线上．若想知道两点A ， B的距离，只需要测量出线段的长度即可．

答案解析收藏纠错 + 选题
14. (2023八上·临海期中) 如图，将长方形纸片进行折叠，ED ， EF为折痕，A与A＇，B与B＇，C与C＇重合，且B＇在A＇E上，若∠AED=25°，则∠BEF的度数为．

答案解析收藏纠错 + 选题
15. (2023八上·临海期中) 如图，△ABC中，AD是△ABC的角平分线，BE是△ABD边AD上的中线，若△ABC的面积是30，AB=9，AC=6，则△ABE的面积是．

答案解析收藏纠错 + 选题
16. (2023八上·临海期中) 在平面直角坐标系中，点A（0，4），B（2，0），在平面内有一点C（不与点B重合），使得△AOC与△AOB全等，则点C的坐标可以为．

答案解析收藏纠错 + 选题

三、解答题（本题共8小题，第17-19题每小题6分，第20-21题每小题8分，第22-23题每小题10分，第24题12分，共66分）

17. (2023八上·临海期中) 如图，校园有两条路OA和OB ，旁边有两块指示牌C ， D ，学校准备在附近安装一盏路灯，要求灯柱的位置P离两块指示牌一样远，并且到两条路的距离相等，请你帮助画出灯柱的位置P（要求尺规作图并保留作图痕迹）．

答案解析收藏纠错 + 选题
18. (2023八上·临海期中) 在棋盘中建立如图的直角坐标系，三颗棋子A ， O ， B的位置如图1，它们分别是（-1，1），（0，0）和（1，0）．
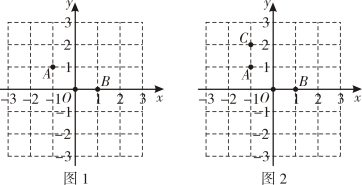
1. （1）如图2，添加棋子C ，使A ， O ， B ， C四颗棋子组成一个轴对称图形，请在图中画出该图形的对称轴；
2. （2）要在其他格点位置添加一颗棋子P ，使A ， O ， B ， P四颗棋子组成一个轴对称图形，请直接写出棋子P的所有可能位置的坐标．
答案解析收藏纠错 + 选题
19. (2023八上·临海期中) 如图，把一个长为10m的梯子AB斜靠在墙上，测得AM＝8m，BM＝6m，梯子沿墙下滑到CD位置，测得∠ABM＝∠DCM ，求梯子下滑的高度AC ．

答案解析收藏纠错 + 选题
20. (2023八上·临海期中) 如果一个多边形的各边都相等，且各内角也都相等，那么这个多边形就叫做正多边形，下图是一组正多边形，观察每个正多边形中∠α的变化情况，解答下列问题．
1. （1）将下面的表格补充完整：
  正多边形的边数
  3
  4
  5
  6
  ……
  n
  ∠α的度数
  60°
  ……
2. （2）根据规律，是否存在一个正n边形，使其中的∠α＝16°？若存在，直接写出n的值；若不存在，请说明理由．
答案解析收藏纠错 + 选题
21. (2023八上·临海期中) 如图，在△ABC中，AB边的垂直平分线l₁交BC于点D ， AC边的垂直平分线l₂交BC于点E ， l₁与l₂相交于点O ．已知△ADE的周长为8cm．
1. （1）求BC的长；
2. （2）分别连接OA ， OB ， OC ，若△OBC的周长为20cm，求OA的长．
答案解析收藏纠错 + 选题
22. (2023八上·临海期中) 如图，在△ABC中，∠ACB=90°，AC=BC ， BE⊥CE于点E ， AD⊥CE于点D ．
1. （1）求证：△ADC≌△CEB ．
2. （2）若AD=5cm，DE=3cm，求BE的长度．
答案解析收藏纠错 + 选题
23. (2023八上·临海期中) 已知△ABC ．
1. （1）如图1，若三角形的内角∠ABC与∠ACB的平分线交于点O ，求证：
  ①∠BOC= $\text{[math]}$ ；
  ②∠BOC= $\text{[math]}$ ；
2. （2）如图2，若三角形的外角∠DBC与∠ECB的平分线交于点O ，试分析∠BOC与∠A有怎样的数量关系，请说明理由；
3. （3）如图3，若三角形的内角∠ABC与外角∠ACD的平分线交于点O ，则∠BOC与∠A的数量关系为．(只写结论，不需证明)
答案解析收藏纠错 + 选题
24. (2023八上·临海期中)
1. （1）某学习小组在探究三角形全等时，发现了下面这种典型的基本图形．如图1，已知：在△ABC中，∠BAC＝90°，AB＝AC ，直线l经过点A ， BD⊥直线l ， CE⊥直线l ，垂足分别为点D、E ．证明：DE＝BD+CE ．
2. （2）组员小明想，如果三个角不是直角，那结论是否会成立呢？如图2，将（1）中的条件改为：在△ABC中，AB＝AC ， D ， A ， E三点都在直线l上，并且有∠BDA＝∠AEC＝∠BAC＝α ，其中α为任意锐角或钝角．请问结论DE＝BD+CE是否成立？如成立，请你给出证明；若不成立，请说明理由．
3. （3）数学老师赞赏了他们的探索精神，并鼓励他们运用这个知识来解决问题：如图3，过△ABC的边AB、AC向外作正方形ABDE和正方形ACFG ， AH是BC边上的高，延长HA交EG于点I ，求证：I是EG的中点．
答案解析收藏纠错 + 选题