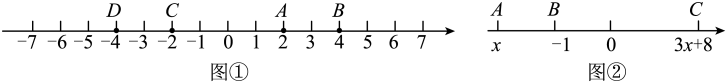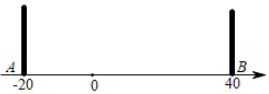
2023年浙教版数学七年级上册6.4线段的和差同步测试（培...

更新时间：2023-11-26 浏览次数：56 类型：同步测试

一、选择题（每题3分，共30分）

1. (2023七上·期末) 如图，D，E顺次为线段AB上的两点，AB=20，C为AD的中点，则下列选项中正确的是（）

A . 若BE-DE=0，则AE-CD= 7 B . 若BE-DE=2，则AE-CD=7 C . 若BE-DE=4，则AE-CD=7 D . 若BE-DE=6，则AE-CD=7

答案解析收藏纠错 + 选题
2. (2023七上·湘潭月考) 已知线段 $\text{[math]}$ ， $\text{[math]}$ 是直线 $\text{[math]}$ 上一点，若 $\text{[math]}$ 是 $\text{[math]}$ 的中点， $\text{[math]}$ 是 $\text{[math]}$ 的中点，则线段 $\text{[math]}$ 的长度是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 或 $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023七上·凤台月考) 如图，已知B，C两点把线段AD从左至右依次分成2：4：3三部分，M是AD的中点，BM＝5cm，则线段MC的长为（）

A . 1cm B . 2cm C . 3cm D . 4cm

答案解析收藏纠错 + 选题
4. (2022七上·汇川期末) 如图，点A，B在线段EF上，点M，N分别是线段EA，BF的中点，EA：AB：BF＝1：2：3，若MN＝8cm，则线段EF的长为（）cm

A . 10 B . 11 C . 12 D . 13

答案解析收藏纠错 + 选题
5. (2022七上·黔西南期末) 已知，点C在直线 AB 上， AC=a ， BC=b ，且 a≠b ，点 M是线段 AB 的中点，则线段 MC的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 或 $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2021七上·南开月考) 如图，A、O、B两点在数轴上对应的数分别为﹣20、0、40，C点在A、B之间，在A、B两点处各放一个挡板，M、N两个小球同时从C处出发，M以2个单位/秒的速度向数轴负方向运动，N以4个单位/秒的速度向数轴正方向运动，碰到挡板后则反方向运动，速度大小不变．设两个小球运动的时间为t秒钟（0＜t＜40），当M小球第一次碰到A挡板时，N小球刚好第一次碰到B挡板．则：①C点在数轴上对应的数为0；②当10＜t＜25时，N在数轴上对应的数可以表示为80﹣4t；③当25＜t＜40时，2MA+NB始终为定值160；④只存在唯一的t值，使3MO＝NO，以上结论正确的有（　　）

A . ①②③④ B . ①③ C . ②③ D . ①②④

答案解析收藏纠错 + 选题
7. (2020七上·江夏期末) 如图， $\text{[math]}$ 、 $\text{[math]}$ 顺次为线段 $\text{[math]}$ 上的两点， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的中点，则 $\text{[math]}$ 的值是（）

A . 5 B . 6 C . 7 D . 8

答案解析收藏纠错 + 选题
8. (2021七上·江干期末) 如图，C、D是线段AB上两点，M、N分别是线段AD、BC的中点，下列结论：
①若AD=BM，则AB=3BD； ②若AC=BD，则AM=BN；③AC-BD=2(MC-DN)；④2MN=AB-CD．其中正确的结论是（）

A . ①②③ B . ③④ C . ①②④ D . ①②③④

答案解析收藏纠错 + 选题
9. (2019七上·台州期末) 如图，C为射线AB上一点，AB＝30，AC比BC的 $\text{[math]}$ 多5，P，Q两点分别从A，B两点同时出发.分别以2单位/秒和1单位/秒的速度在射线AB上沿AB方向运动，运动时间为t秒，M为BP的中点，N为QM的中点，以下结论：①BC＝2AC；②AB＝4NQ；③当PB＝ $\text{[math]}$ BQ时，t＝12，其中正确结论的个数是（）

A . 0 B . 1 C . 2 D . 3

答案解析收藏纠错 + 选题
10. (2019七上·龙岗期中) 已知多项式 $\text{[math]}$ 的常数项是a，次数是b，且a，b两个数轴上所对应的点分别为A、B，若点A、点B同时沿数轴向正方向运动，点A的速度是点B的2倍，且3秒后， $\text{[math]}$ ，求点B的速度为（）

A . $\text{[math]}$ B . $\text{[math]}$ 或 $\text{[math]}$ C . $\text{[math]}$ 或 $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（每题4分，共24分）

11. (2023七上·通川期末) 在直线 $\text{[math]}$ 上取 $\text{[math]}$ ， $\text{[math]}$ 两点，使 $\text{[math]}$ ，再在直线 $\text{[math]}$ 上取一点 $\text{[math]}$ ，使 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分别是 $\text{[math]}$ ， $\text{[math]}$ 的中点，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
12. (2022七上·萧山期末) 如图，点 $\text{[math]}$ ， $\text{[math]}$ 是直线 $\text{[math]}$ 上的两点，点 $\text{[math]}$ ， $\text{[math]}$ 在直线 $\text{[math]}$ 上且点 $\text{[math]}$ 在点 $\text{[math]}$ 的左侧，点 $\text{[math]}$ 在点 $\text{[math]}$ 的右侧， $\text{[math]}$ ， $\text{[math]}$ .若 $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
13. (2021七上·杭州期末) 如图，线段 $\text{[math]}$ 表示一条已对折的绳子，现从 $\text{[math]}$ 点处将绳子剪断，剪断后的各段绳子中最长的一段为 $\text{[math]}$ ，若 $\text{[math]}$ ，则原来绳长 $\text{[math]}$ .

答案解析收藏纠错 + 选题
14. (2023·海曙竞赛) 如图所示：已知 $\text{[math]}$ ， $\text{[math]}$ ，现有 $\text{[math]}$ 点和 $\text{[math]}$ 点分别从 $\text{[math]}$ ， $\text{[math]}$ 两点出发相向运动， $\text{[math]}$ 点速度为 $\text{[math]}$ ， $\text{[math]}$ 点速度为 $\text{[math]}$ ，当 $\text{[math]}$ 到达 $\text{[math]}$ 点后掉头向 $\text{[math]}$ 点运动， $\text{[math]}$ 点在向 $\text{[math]}$ 的运动过程中经过 $\text{[math]}$ 点时，速度变为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 两点中有一点到达 $\text{[math]}$ 点时，全部停止运动，那么经过 $\text{[math]}$ 后 $\text{[math]}$ 的距离为 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
15. (2020七上·重庆月考) 如图，数轴上有两点 $\text{[math]}$ ，点C从原点O出发，以每秒 $\text{[math]}$ 的速度在线段 $\text{[math]}$ 上运动，点D从点B出发，以每秒 $\text{[math]}$ 的速度在线段 $\text{[math]}$ 上运动.在运动过程中满足 $\text{[math]}$ ，若点M为直线 $\text{[math]}$ 上一点，且 $\text{[math]}$ ，则 $\text{[math]}$ 的值为.

答案解析收藏纠错 + 选题
16. (2023七上·金东期末) 有一无弹性细线，拉直时测得细线 $\text{[math]}$ 长为 $\text{[math]}$ ，现进行如下操作：1.在细线上任取一点 $\text{[math]}$ ；2.将细线折叠，使点 $\text{[math]}$ 与点 $\text{[math]}$ 重合，记折点为点 $\text{[math]}$ ；3.将细线折叠，使点 $\text{[math]}$ 与点 $\text{[math]}$ 重合，记折点为点 $\text{[math]}$ .
1. （1）如图， $\text{[math]}$ 的长为 $\text{[math]}$ ；
2. （2）继续进行折叠，使点 $\text{[math]}$ 与点 $\text{[math]}$ 重合，并把 $\text{[math]}$ 点和与其重叠的 $\text{[math]}$ 点处的细线剪开，使细线分成长为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的三段 $\text{[math]}$ ，当 $\text{[math]}$ ，则细线未剪开时 $\text{[math]}$ 的长为 $\text{[math]}$ .
答案解析收藏纠错 + 选题

三、解答题（共8题，共66分）

17. (2021七上·紫阳期末) 如图，平面上有四个点 $\text{[math]}$ ，按照以下要求作图并解答问题：
1. （1） ①作直线 $\text{[math]}$ ；
  ②作射线 $\text{[math]}$ 交直线 $\text{[math]}$ 于点 $\text{[math]}$ ；
  
  ③连接 $\text{[math]}$ 交于点 $\text{[math]}$ ；
2. （2）若图中 $\text{[math]}$ 是 $\text{[math]}$ 的一个三等分点， $\text{[math]}$ 已知线段 $\text{[math]}$ 上所有线段之和为 $\text{[math]}$ 求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
18. (2020七上·大连期末) 如图：
1. （1）如图1，已知平面上A，B，C三点，请按照下列语句画出图形．
  ①连接 $\text{[math]}$ ；
  
  ②画射线 $\text{[math]}$ ；
  
  ③画直线 $\text{[math]}$ ；
2. （2）如图2，已知线段 $\text{[math]}$ ．
  ①画图：延长 $\text{[math]}$ 到C，使 $\text{[math]}$ ；
  
  ②若D为 $\text{[math]}$ 的中点，且 $\text{[math]}$ ，求线段 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
19. (2020七上·延庆期末) 如图
1. （1）如图1，平面上有3个点A，B，C．
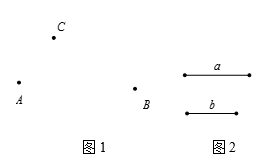
  ①画直线AB；画射线BC；画线段AC；
  
  ②过点C作AB的垂线，垂足为点D；
  
  ③量出点C到直线AB的大约距离．
2. （2）尺规作图：
  已知：线段a，b，如图2．
  
  求作：一条线段MN，使它等于2a－b．（不写作法，保留作图痕迹）
答案解析收藏纠错 + 选题
20. (2020七上·延庆期末) 已知：点M，N，P在同一条直线上，线段MN＝6，且线段PN＝2．
1. （1）若点P在线段MN上，求MP的长；
2. （2）若点P在射线MN上，点A是MP的中点，求线段AP的长．
答案解析收藏纠错 + 选题
21. (2023七上·桂平期末) 如图，在平面内有三个点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）按下面的要求作图：（要求：利用尺规，不写画法，保留作图痕迹，不写结论）
  ①连接 $\text{[math]}$ ， $\text{[math]}$ ，作射线 $\text{[math]}$ ；
  
  ②在射线 $\text{[math]}$ 上作线段 $\text{[math]}$ ，使 $\text{[math]}$ ．
2. （2）已知 $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 的中点．将点 $\text{[math]}$ 标在（1）所画的图中，并求线段 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
22. (2023七上·苏州月考) 如图，在数轴上有A，B两点，其中点A在点B的左侧，已知点B对应的数为4，点A对应的数为a.
1. （1）若a＝ $\text{[math]}$ ×72，则线段AB的长为（直接写出结果）.
2. （2）若点C在射线AB上（不与A，B重合），且2AC-3BC＝6，求点C对应的数（结果用含a的式子表示）.
3. （3）若点M在线段AB之间，点N在点A的左侧（M、N均不与A、B重合），且AM-BM＝2.当 $\text{[math]}$ ＝3，BN＝6BM时.求a的值.
答案解析收藏纠错 + 选题
23. (2020七上·成都期末) 如果一点在由两条公共端点的线段组成的一条折线上且把这条折线分成长度相等的两部分，这点叫做这条折线的“折中点”．如图，点D是折线A﹣C﹣B的“折中点”，请解答以下问题：
1. （1）当AC＞BC时，点D在线段上；当AC＝BC时，点D与重合；当AC＜BC时，点D在线段上；
2. （2）若AC＝18cm，BC＝10cm，若∠ACB=90°，有一动点P从C点出发，在线段CB上向点B运动，速度为2cm/s，设运动时间是t（s），求当t为何值，三角形PCD 的面积为10 $\text{[math]}$ ？
3. （3）若E为线段AC中点，EC＝8cm，CD＝6cm，求CB的长度．
答案解析收藏纠错 + 选题
24. (2021七上·萍乡期末) 阅读理解：
【探究与发现】在一次数学探究活动中，数学兴趣小组发现可以通过“两数的差”来表示“数轴上两点间的距离”，如图①中三条线段的长度可表示为： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， …结论：数轴上任意两点表示的数分别为a，b（ $\text{[math]}$ ），则这两个点间的距离为 $\text{[math]}$ （即：用较大的数减去较小的数）．
【理解与应用】
1. （1）在数轴上分别有点M、N、H，其中M、N表示的数分别为 $\text{[math]}$ ， 2020，点H为线段MN的中点，若点H表示的数为m，求m的值；
2. （2）如图②，数轴上点A，B，C表示的数分别为x， $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ，求A，C分别表示什么数？
3. （3）在（2）的条件下，图②的数轴上是否存在点D，使 $\text{[math]}$ ？若存在，请直接写出点D表示的数，若不存在，请说明理由．（点D不与点A、B、C重合）．
答案解析收藏纠错 + 选题