2023年浙教版数学七年级上册第六章图形的初步知识单元测...

更新时间：2023-11-26 浏览次数：107 类型：单元试卷

一、选择题（每题3分，共30分）

1. (2023七上·龙岗期中) 用一个平面去截一个正方体，则截面的形状不可能为（）

A . 等腰三角形 B . 梯形 C . 正七边形 D . 五边形

答案解析收藏纠错 + 选题
2. (2022七上·乌鲁木齐期中) 如果线段 $\text{[math]}$ ， $\text{[math]}$ ，那么下面说法中正确的是（）

A . M点在线段 $\text{[math]}$ 上 B . M点在直线 $\text{[math]}$ 上 C . M点在直线 $\text{[math]}$ 外 D . M点可能在直线 $\text{[math]}$ 上，也可能在直线 $\text{[math]}$ 外

答案解析收藏纠错 + 选题
3. (2023七上·海曙期末) 把弯曲的道路改直就能缩短路程，下列数学语言解释正确的是（）

A . 垂线段最短 B . 两点确定一条直线 C . 两点之间线段最短 D . 对顶角相等

答案解析收藏纠错 + 选题
4. (2023七上·洛川期末) 已知A，B，C是同一直线上的三个点，且AB＝9cm，BC＝4cm，D是BC的中点，则AD的长是（）

A . 13cm B . 7cm C . 11cm D . 7cm或11cm

答案解析收藏纠错 + 选题
5. (2023七上·达川期末) 如图， $\text{[math]}$ 是直线， $\text{[math]}$ 是直线上一点， $\text{[math]}$ 、 $\text{[math]}$ 是两条射线，则图中小于平角的角有（）

A . 3个 B . 4个 C . 5个 D . 6个

答案解析收藏纠错 + 选题
6.
如图，如果∠CAE＞∠BAD，那么下列说法中一定正确的是（　　）

A . ∠BAC＞∠CAD B . ∠DAE＞∠CAD C . ∠CAE＜∠BAC+∠DAE D . ∠BAC＜∠DAE

答案解析收藏纠错 + 选题
7. (2021七上·海曙期末) 如图，将三个三角板直角顶点重叠在一起，公共的直角顶点为点 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，那么 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023七上·义乌期末) 下列四个图中，能表示线段 $\text{[math]}$ 的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
9. (2023七上·鄞州期末) 下列说法中，正确的是（）

A . 相等的角是对顶角 B . 若AB=BC，则点B是线段AC的中点 C . 在同一平面内，过一点有且仅有一条直线垂直于已知直线 D . 一个锐角的补角大于等于该锐角的余角

答案解析收藏纠错 + 选题
10. (2021七上·嘉兴期末) 已知 $\text{[math]}$ 与 $\text{[math]}$ 满足 $\text{[math]}$ ，下列式子表示的角：① $\text{[math]}$ ：② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ 中，其中是 $\text{[math]}$ 的余角的是（）

A . ①② B . ①③ C . ②④ D . ③④

答案解析收藏纠错 + 选题

二、填空题（每题4分，共24分）

11. (2024七上·宝安月考) 钟表上的时针转动一周形成一个圆面，这说明了．

答案解析收藏纠错 + 选题
12. 如图，小亮将一个衣架固定在墙上，他在衣架两端各用一个钉子进行固定，请你用数学知识解释他这样操作的原因是

答案解析收藏纠错 + 选题
13. (2021七上·东台期末) 下列生产和生活现象：①用两个钉子就可以把木条固定在墙上；②把弯曲的公路改直，就能缩短路程；③植树时，只要确定两棵树的位置，就能确定同一行树所在的直线；④从 $\text{[math]}$ 地到 $\text{[math]}$ 地架设电线，总是尽可能沿着线段 $\text{[math]}$ 架设.其中能用“两点之间，线段最短”来解释的现象有.（填序号）

答案解析收藏纠错 + 选题
14. (2023七上·海曙期末) 已知线段AB=12，C是线段AB上一点，且BC=2，点D在射线AB上，若DA=4DC，则BD的长为.

答案解析收藏纠错 + 选题
15. (2021七上·义乌期末) 如图，将量角器的中心与 $\text{[math]}$ 的顶点重合，读出射线OA，OB分别经过刻度18和140，把 $\text{[math]}$ 绕点O顺时针方向旋转到 $\text{[math]}$ ，读出 $\text{[math]}$ 的平分线OC经过刻度32，则 $\text{[math]}$ 的平分线经过的刻度是．

答案解析收藏纠错 + 选题
16. (2021七上·东阳期末) 如图，将两块直角三角尺的直角顶点C叠放在一起．若 $\text{[math]}$ ，则∠ACB的度数为．

答案解析收藏纠错 + 选题

三、解答题（共9题，共66分）

17. (2021七上·越秀期末) 如图，在平面内有 $\text{[math]}$ 三点．
1. （1）画直线 $\text{[math]}$ ；画射线 $\text{[math]}$ ；画线段 $\text{[math]}$ ；
2. （2）在线段 $\text{[math]}$ 上任取一点 $\text{[math]}$ （不同于 $\text{[math]}$ ），连接 $\text{[math]}$ ，并延长 $\text{[math]}$ 至点 $\text{[math]}$ ，使 $\text{[math]}$ ；
3. （3）数一数，此时图中共有多少条线段？多少条射线？
答案解析收藏纠错 + 选题
18. (2023七上·大竹期末) 如图，点P是线段AB上任一点，AB＝12cm，C，D两点分别从点P，B同时向点A运动，且点C的运动速度为2cm/s，点D的运动速度为3cm/s，运动的时间为t s．
1. （1）若AP＝8cm，
  ①运动1s后，求CD的长；②当点D在线段PB上运动时，试说明AC=2CD；
2. （2）如果t＝2s时，CD＝1cm，试探索AP的值．
答案解析收藏纠错 + 选题
19. (2024七下·廉江月考) 如图，直线AB、CD相交于点O，OM⊥AB.
1. （1）若∠1＝∠2，证明：ON⊥CD；
2. （2）若∠1＝ $\text{[math]}$ ∠BOC，求∠BOD的度数.
答案解析收藏纠错 + 选题
20. 如图是小明用七巧板拼出的图案．
1. （1）请赋予该图形一个积极的含义；
2. （2）请你找出图中二组平行线段和二对互相垂直的线段，用符号表示他们；
3. （3）找出图中一个锐角，一个钝角，一个直角，将它们表示出来，并指出它们的度数．
答案解析收藏纠错 + 选题
21. (2021七上·金东期末) 定义：在一个已知角内部，一条线分已知角成两个新角，其中一个角度数为另个角度数的两倍，我们把这条线叫做这个已知角的三等分线．
1. （1）如图，已知∠AOB＝120°，若OC是∠AOB三等分线，求∠AOC的度数．
2. （2）点O在线段AB上（不含端点A，B），在直线AB同侧作射线OC，OD．设∠AOC＝3t，∠BOD＝5t．
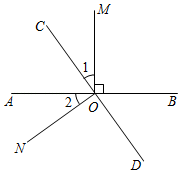
  ①当OC是∠AOD的三等分线时，求t的值．
  ②当OC是∠BOD的三等分线时，求∠BOD的度数．
答案解析收藏纠错 + 选题
22. (2023七上·嘉兴期末) 定义：从一个角的顶点引出的一条射线，把这个角分成1：2两部分，这条射线叫做这个角的内倍分线．
1. （1）如图1，OM是∠AOB的一条内倍分线，满足∠BOM=2∠AOM，若∠AOB =45°，求∠AOM的度数．
2. （2）已知∠AOB=60°，把一块含有60角的三角板COD按如图2叠放．将三角板COD绕顶点O以2度/秒的速度按顺时针方向旋转秒(0<t<180) 。
  ①t为何值时，射线OC是∠AOD的内倍分线；
  ②在三角板COD转动的同时，射线OB以每秒n(0<n<1)度的速度绕O点逆时针方向旋转至OB'，在旋转过程中存在OB'恰好同时是∠AOD，∠AOC的内倍分线，请直接写出n的值．
答案解析收藏纠错 + 选题
23. (2021七上·嘉兴期末) 将直角三角板OMN的直角顶点О放在直线AB上，射线OC平分∠AON.
1. （1）如图，若∠BON=60°，求∠COM的度数；
2. （2）将直角三角板OMN绕顶点О按逆时针方向旋转，在旋转过程中：
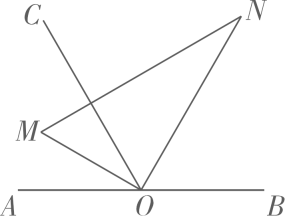
  ①当∠BON=140°时，求∠COM的度数：
  
  ②直接写出∠BON和∠COM之间的数量关系.
答案解析收藏纠错 + 选题
24. (2021七上·鄞州期末) 如图，直线 $\text{[math]}$ ， $\text{[math]}$ 相交于点 $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ .
1. （1）【基础尝试】
  如图1，若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数；
2. （2）【画图探究】
  作射线 $\text{[math]}$ ，设 $\text{[math]}$ ，请你利用图2画出图形，探究 $\text{[math]}$ 与 $\text{[math]}$ 之间的关系，结果用含 $\text{[math]}$ 的代数式表示 $\text{[math]}$ .
3. （3）【拓展运用】
  在第（2）题中， $\text{[math]}$ 可能和 $\text{[math]}$ 互补吗？请你作出判断并说明理由.
答案解析收藏纠错 + 选题
25. (2023七上·兰溪期末) 问题提出：
如图1，A、B、C、D表示四个村庄，村民们准备合打一口水井.
1. （1）问题解决：
  若水井的位置现有P、Q两种选择方案.点P在线段 $\text{[math]}$ 上，点Q在线段 $\text{[math]}$ 上，哪一种方案的水井到各村庄的距离总和较小？请说明你判断的理由.
2. （2）你能给出一种使水井到各村庄的距离之和最小的方案吗？若能，请图2中标出水井的位置点M，并说明理由.
3. （3）问题拓展：
  如果（2）问中找出的水井经过招标，由两个工程队修建（不存在同时修建）. 已知甲工程队单独完成需要80天，乙工程队单独完成需要120天，且甲工程队比乙工程队每天多修建 $\text{[math]}$ .
  问水井要修建几米？
4. （4）若甲工程队每天的施工费为0.5万元，乙工程队每天的费用是0.25万元，为了缩短工期和节约资金，则甲工程队最多施工几天才能使工程款不超过35万元？（甲、乙两队的施工时间不足一天按一天算）.
答案解析收藏纠错 + 选题