四川省成都市邛崃高埂中学学区2023-2024学年八年级上学...

更新时间：2024-01-05 浏览次数：39 类型：月考试卷

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）

1. (2023八上·邛崃月考) 下列实数中，无理数是（）

A . 3.1415926 B . ﹣0.202002000 C . D .

答案解析收藏纠错 + 选题
2. (2023·新兴模拟) 如图，以直角三角形的三边为边向外作正方形，根据图中数据，可得出正方形A的面积是（）

A . 12 B . 24 C . 30 D . 10

答案解析收藏纠错 + 选题
3. (2023八上·邛崃月考) 下列说法正确的是（）

A . $\text{[math]}$ 的算术平方根是2 B . 9的立方根是3 C . $\text{[math]}$ 的平方根是 $\text{[math]}$ D . $\text{[math]}$ 是 $\text{[math]}$ 的一个平方根

答案解析收藏纠错 + 选题
4. (2024七下·浦北月考) 已知 $\text{[math]}$ ，则 $\text{[math]}$ 的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023八上·邛崃月考) 若的整数部分为x ，小数部分为y ，则（x+）y的值是（）

A . B . 3 C . D . ﹣3

答案解析收藏纠错 + 选题
6. (2023八上·邛崃月考) 下列命题中，假命题是（）

A . 实数和数轴上的点是一一对应的 B . $\text{[math]}$ 是一组勾股数 C . 有公共顶点且相等的两个角是对顶角 D . 函数 $\text{[math]}$ 中自变量 $\text{[math]}$ 的取值范围是 $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023八上·邛崃月考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 和 $\text{[math]}$ 均为等腰直角三角形，且面积之和为 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . 25 C . $\text{[math]}$ D . 10

答案解析收藏纠错 + 选题
8. (2023八上·邛崃月考) 在△ABC中，三边长分别为a、b、c ，且a+c＝2b ， c﹣a＝b ，则△ABC是（）

A . 直角三角形 B . 等边三角形 C . 等腰三角形 D . 等腰直角三角形

答案解析收藏纠错 + 选题

二、填空题（本大题共5个小题，每小题4分，共20分）

9. (2023八上·邛崃月考) $\text{[math]}$ 的平方根； $\text{[math]}$ 的立方根．

答案解析收藏纠错 + 选题
10. (2023八上·邛崃月考) 如图，有一个水池，水面是一个边长为14尺的正方形，在水池正中央有一根芦苇，它高出水面1尺，如果把这根芦苇拉向水池一边的中点，它的顶端恰好到达池边的水面．则水的深度是尺

答案解析收藏纠错 + 选题
11. (2024八下·南明月考) 已知Rt△ABC中，∠C=90°，a+b=14cm，c=10cm，则Rt△ABC的面积等于 cm² ．

答案解析收藏纠错 + 选题
12. (2023八上·邛崃月考) 比较大小：2 $\text{[math]}$ $\text{[math]}$ ， $\text{[math]}$ $\text{[math]}$ ．

答案解析收藏纠错 + 选题
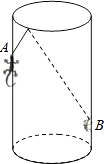
13. (2023八上·邛崃月考) 如图，圆柱形容器中，高为1.2m，底面周长为1m，在容器内壁离容器底部0.3m的点B处有一蚊子，此时一只壁虎正好在容器外壁，离容器上沿0.3m与蚊子相对的点A处，则壁虎捕捉蚊子的最短距离为 m（容器厚度忽略不计）．

答案解析收藏纠错 + 选题

三、解答题（本大题共5个小题，共48分，其中14题12分，15-16题每题8分，17-18题每题10分）

14. (2023八上·邛崃月考) 计算：
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
3. （3） $\text{[math]}$
4. （4） $\text{[math]}$
答案解析收藏纠错 + 选题
15. (2024八下·青山湖月考) 聊城市在创建“全国文明城市”期间，某小区在临街的拐角清理出了一块可以绿化的空地．如图，经技术人员的测量，已知AB＝9m，BC＝12m，CD＝17m，AD＝8m，∠ABC＝90°．若平均每平方米空地的绿化费用为150元，试计算绿化这片空地共需花费多少元？

答案解析收藏纠错 + 选题
16. (2023八上·邛崃月考) 已知 $\text{[math]}$ 的平方根是 $\text{[math]}$ ， $\text{[math]}$ 的立方根是 $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的整数部分；
1. （1）直接写出 $\text{[math]}$ 的值；
2. （2）若 $\text{[math]}$ 是 $\text{[math]}$ 的小数部分，求 $\text{[math]}$ 的算术平方根．
答案解析收藏纠错 + 选题
17. (2023八上·邛崃月考) 对于整数n ，定义[ $\text{[math]}$ ]为不大于 $\text{[math]}$ 的最大整数，例如：[ $\text{[math]}$ ]＝1，[ $\text{[math]}$ ]＝2，[ $\text{[math]}$ ]＝2．
1. （1）直接写出[ $\text{[math]}$ ]的值；
2. （2）显然，当[ $\text{[math]}$ ]＝1时，n＝1，2或3．
  ①当[ $\text{[math]}$ ]＝2时，直接写出满足条件的n的值；
  ②当[ $\text{[math]}$ ]＝10时，求满足条件的n的个数；
3. （3）对72进行如下操作：72 $\text{[math]}$ [ $\text{[math]}$ ]＝8 $\text{[math]}$ [ $\text{[math]}$ ]＝2 $\text{[math]}$ [ $\text{[math]}$ ]＝1，即对72进行3次操作后变为1，类似地：①对25进行 ▲ 次操作后变为2；
  ②对整数m进行3次操作后变为2，直接写出m的最大值．
答案解析收藏纠错 + 选题
18. (2023八上·邛崃月考) 阅读材料，解决问题：
我们可以在网格纸中通过构造三角形的方法来比较无理数的大小，例如在图1中，正方形网格纸中，每个小正方形的边长都是1，线段AB的长度为 $\text{[math]}$ ，线段BC的长度为 $\text{[math]}$ ，显然， $\text{[math]}$ ．
1. （1）试比较 $\text{[math]}$ 与 $\text{[math]}$ 的大小，并说明理由；
2. （2）请在图2中尝试用构造图形的方法比较 $\text{[math]}$ 与 $\text{[math]}$ 的大小，在图3中尝试用构造图形的方法比较 $\text{[math]}$ 与 $\text{[math]}$ 的大小；
3. （3）请运用以上的构图思想，在图4中构图，并求出 $\text{[math]}$ 的最小值．
答案解析收藏纠错 + 选题

四、填空题（本大题共5个小题，每小题4分，共20分）

19. (2023八上·邛崃月考) 据说，我国著名数学家华罗庚在一次出国访问途中，看到飞机上邻座的乘客阅读的杂志上有一道智力题：一个数是59319，希望求它的立方根．华罗庚脱口而出：39．邻座的乘客十分惊奇，忙问计算的奥秘．华罗庚给出了如下方法：（1）由 $\text{[math]}$ ， $\text{[math]}$ ，确定 $\text{[math]}$ 是两位数；（2）由59319个位上的数是9，确定 $\text{[math]}$ 个位上的数是9；（3）划去59319后面的三位319得到59，而 $\text{[math]}$ ， $\text{[math]}$ ，由此确定 $\text{[math]}$ 十位上的数是3．请你类比上述过程，确定21952的立方根是．

答案解析收藏纠错 + 选题
20. (2023八上·邛崃月考) 已知a、b为非零实数，且 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
21. (2023八上·邛崃月考) 如图，在直角三角形纸片 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 在边 $\text{[math]}$ 上，以 $\text{[math]}$ 为折痕将 $\text{[math]}$ 折叠得到 $\text{[math]}$ ， $\text{[math]}$ 与边 $\text{[math]}$ 交于点 $\text{[math]}$ ，当 $\text{[math]}$ 时， $\text{[math]}$ 的长是．

答案解析收藏纠错 + 选题
22. (2023八上·邛崃月考) 如图， $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 为四个全等的直角三角形， $\text{[math]}$ 与 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 分别交于点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ，且满足 $\text{[math]}$ ，则两个阴影部分的面积和与四边形 $\text{[math]}$ 面积的比值为．

答案解析收藏纠错 + 选题
23. (2023八上·邛崃月考) 如图，点P是矩形 $\text{[math]}$ 内任意一点，连结 $\text{[math]}$ ，记 $\text{[math]}$ ，则下列各结论一定成立的有（填序号）
① $\text{[math]}$ ；②若 $\text{[math]}$ ，则 $\text{[math]}$ ；
③ $\text{[math]}$ ；④ $\text{[math]}$ ，则P在对角线 $\text{[math]}$ 上

答案解析收藏纠错 + 选题

五、解答题（本小题共3个小题，共30分，其中24题8分，25题10分，26题12分）

24. (2023八上·邛崃月考) 台风是一种自然灾害，它以台风中心为圆心，在周围数十千米范围内形气旋风暴，有极强的破坏力，此时某台风中心在海域B处，在沿海城市A的正南方向240千米，其中心风力为12级，每远离台风中心25千米，台风就会减弱一级，如图所示，该台风中心正以20千米/时的速度沿北偏东30°方向向C移动，且台风中心的风力不变，若城市所受风力达到或超过4级，则称受台风影响．
试问：
1. （1） A城市是否会受到台风影响？请说明理由．
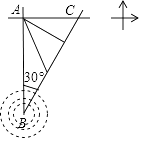
2. （2）若会受到台风影响，那么台风影响该城市的持续时间有多长？
3. （3）该城市受到台风影响的最大风力为几级？
答案解析收藏纠错 + 选题
25. (2023八上·邛崃月考) 先阅读下列解答过程，然后再解答：小芳同学在研究化简 $\text{[math]}$ 中发现：首先把 $\text{[math]}$ 化为 $\text{[math]}$ ﹐由于 $\text{[math]}$ ， $\text{[math]}$ ，即： $\text{[math]}$ ， $\text{[math]}$ ，所以 $\text{[math]}$ ，
问题：
1. （1）填空： $\text{[math]}$ ， $\text{[math]}$ ﹔
2. （2）进一步研究发现：形如 $\text{[math]}$ 的化简，只要我们找到两个正数a ， b（ $\text{[math]}$ ），使 $\text{[math]}$ ， $\text{[math]}$ ，即 $\text{[math]}$ ， $\text{[math]}$ ﹐那么便有： $\text{[math]}$ ．
3. （3）化简： $\text{[math]}$ （请写出化简过程）
答案解析收藏纠错 + 选题
26. (2023八上·邛崃月考) 如图1，在△ABC和△ADE中，∠DAE=∠BAC，AD=AE，AB=AC.
1. （1）求证：△ABD≌△ACE；
2. （2）如图2，在△ABC和△ADE中，∠DAE=∠BAC，AD=AE，AB=AC，∠ADB=90°，点E在△ABC内，延长DE交BC于点F，求证：点F是BC中点；
3. （3） △ABC为等腰三角形，∠BAC=120°，AB=AC，点P为△ABC所在平面内一点，∠APB=120°，AP=2，BP=4，请直接写出 CP的长.
答案解析收藏纠错 + 选题