甘肃省兰州市教育局第四片区2023-2024学年九年级上学期...

更新时间：2024-01-08 浏览次数：27 类型：期中考试

一、选择题（本大题共12小题，每小题3分，共36分，在每小题给出的四个选项中，只有一项是符合题目要求的）

1. (2024九下·仁寿期中) 方程 $\text{[math]}$ 的解是（ $\text{[math]}$

A . $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023九上·兰州期中) 将方程 $\text{[math]}$ 的形式，指出 $\text{[math]}$ 分别是（）

A . 1和3 B . -1和3 C . 1和4 D . -1和4

答案解析收藏纠错 + 选题
3. (2024八下·利津期末) 已知点P是线段AB的黄金分割点（AP＞PB），AB=4，那么AP的长是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024九上·重庆市开学考) 下列命题中，不正确的是（　　）

A . 顺次连接菱形各边中点所得的四边形是矩形 B . 有一个角是直角的菱形是正方形 C . 对角线相等且垂直的四边形是正方形 D . 有一个角是60°的等腰三角形是等边三角形

答案解析收藏纠错 + 选题
5. (2023九上·兰州期中) 顺次连接对角线相等的四边形各边中点所得四边形是（）

A . 矩形 B . 平行四边形 C . 菱形 D . 任意四边形

答案解析收藏纠错 + 选题
6. (2023九上·兰州期中) 若关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 有一个根为0，则 $\text{[math]}$ 的值（）

A . 0 B . 1或2 C . 1 D . 2

答案解析收藏纠错 + 选题
7. (2023九上·兰州期中) 根据下列表格对应值：
x 3.24 3.25 3.26
ax²+bx+c -0.02 0.01 0.03
判断关于x的方程 $\text{[math]}$ $\text{[math]}$ 的一个解x的范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024九下·天山模拟) 一个不透明的盒子里有n个除颜色外其它完全相同的小球，其中有6个黄球．每次摸球前先将盒子里的球摇匀，任意摸出一个球记下颜色后在放回盒子，通过大量重复摸球实验后发现，摸到黄球的频率稳定在30%，那么可以推算出n大约是( )

A . 6 B . 10 C . 18 D . 20

答案解析收藏纠错 + 选题
9. (2024九上·惠来期末) 如图，每个小正方形的边长均为1，则下列图形中的三角形（阴影部分）与△A₁B₁C₁相似的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
10. (2023九上·兰州期中) 连续掷三枚质地均与的硬币，三枚硬币都是正面朝上的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2023九上·兰州期中) 某钢铁厂今年1月份钢产量为5000吨，3月份上升到7200吨，设平均每月增长的百分率为 $\text{[math]}$ ，据题意得方程（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
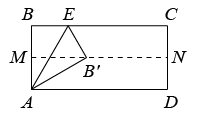
12. (2023九上·兰州期中) 如图所示，将矩形ABCD纸对折，设折痕为MN ，再把B点叠在折痕线MN上，（如图点B′），若 $\text{[math]}$ ，则折痕AE的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 2 D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（本大题共4小题，每小题3分，共12分）

13. (2023九上·兰州期中) 王芳抛一枚硬币10次，有8次正面朝上，当她抛第11次，正面朝上的概率．

答案解析收藏纠错 + 选题
14. (2024八上·景泰期中) 已知菱形一条对角线为长8 $\text{[math]}$ cm，周长是24 cm，则这个菱形的面积是

答案解析收藏纠错 + 选题
15. (2024八上·景泰期中) 关于x的一元二次方程 $\text{[math]}$ 有实数根，则k的取值范围是

答案解析收藏纠错 + 选题
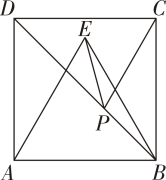
16. (2023九上·兰州期中) 如图，正方形ABCD的面积为16，△ABE是等边三角形，点E在正方形ABCD内，在对角线BD上有一点P，使PC+PE的和最小，则这个最小值为.

答案解析收藏纠错 + 选题

三、计算题（本大题共12小题，共72分．解答时写出必要的文字说明、证明过程或演算步骤）

17. (2023九上·兰州期中) 解方程： $\text{[math]}$

答案解析收藏纠错 + 选题
18. (2023九上·兰州期中) 解方程 $\text{[math]}$

答案解析收藏纠错 + 选题
19. (2024九上·潮阳期末) 解方程： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
20. (2023九上·兰州期中) 解方程： $\text{[math]}$

答案解析收藏纠错 + 选题
21. (2023九上·兰州期中) 如图，矩形 $\text{[math]}$ 的对角线 $\text{[math]}$ 、 $\text{[math]}$ 交于点 $\text{[math]}$ ，分别过 $\text{[math]}$ 、 $\text{[math]}$ 作 $\text{[math]}$ 、 $\text{[math]}$ 的平行线交于点 $\text{[math]}$ ，求证：四边形 $\text{[math]}$ 是菱形

答案解析收藏纠错 + 选题
22. (2023九上·兰州期中) 如图所示，要在20米宽，32米长的矩形耕地上修筑同样宽的三条小路（两条纵向，一条横向，横向与纵向互相垂直），把耕地分成大小不等的六块花田，要使花田面积为 $\text{[math]}$ ，则道路应修多宽？

答案解析收藏纠错 + 选题
23. (2023九上·兰州期中) 小敏的爸爸买了某项体育比赛的一张门票，她和哥哥两人都很想去观看．可门票只有一张，读九年级的哥哥想了一个办法，拿了8张扑克牌，将数字为2，3，5，9的四张牌给小敏，将数字为4，6，7，8的四张牌留给自己，并按如下游戏规则进行：小敏和哥哥从各自的四张牌中随机抽出一张，然后将两人抽出的两张扑克牌数字相加，如果和为偶数，则小敏去；如果和为奇数，则哥哥去．
1. （1）请用画树形图或列表的方法求小敏去看比赛的概率；
2. （2）哥哥设计的游戏规则公平吗？若公平，请说明理由；若不公平，请你设计一种公平的游戏规则．
答案解析收藏纠错 + 选题
24. (2023九上·兰州期中) 在平面直角坐标系中，分别描出点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）试判断四边形 $\text{[math]}$ 的形状；
2. （2）若 $\text{[math]}$ 两点不动，你能通过变动点 $\text{[math]}$ 的位置使四边形 $\text{[math]}$ 成为正方形吗？若能，请写出变动后的点 $\text{[math]}$ 的坐标．
答案解析收藏纠错 + 选题
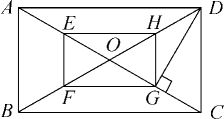
25. (2023九上·兰州期中) 如图，O是矩形ABCD的对角线的交点，E，F，G，H分别是OA，OB，OC，OD上的点，且AE＝BF＝CG＝DH.
1. （1）求证：四边形EFGH是矩形；
2. （2）若E，F，G，H分别是OA，OB，OC，OD的中点，且DG⊥AC，OF＝2cm，求矩形ABCD的面积．
答案解析收藏纠错 + 选题
26. (2023九上·兰州期中) 某水果批发商场经销一种高档水果，如果每千克盈利10元，每天可售出500千克，经市场调查发现，在进货价不变的情况下，若每千克涨价1元，日销量减少20千克，现该商场要保证每天盈利6000元，同时又要使顾客得到实惠，那么每千克应涨价多少元？

答案解析收藏纠错 + 选题
27. (2023九上·兰州期中) 如图， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 上移动，以 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为顶点的三角形与 $\text{[math]}$ 相似时，求 $\text{[math]}$ 的长．

答案解析收藏纠错 + 选题
28. (2023九上·兰州期中) 如图，平行四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．对角线 $\text{[math]}$ 相交于点 $\text{[math]}$ ，将直线 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转，分别交 $\text{[math]}$ 于点 $\text{[math]}$ ．
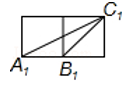
1. （1）【问题解决】
  证明：当旋转角为 $\text{[math]}$ 时，四边形 $\text{[math]}$ 是平行四边形；
2. （2）【类比探究】
  试说明在旋转过程中，线段 $\text{[math]}$ 与 $\text{[math]}$ 总保持相等；
3. （3）【拓展应用】
  在旋转过程中，四边形 $\text{[math]}$ 可能是菱形吗？如果不能，请说明理由；如果能，说明理由并求出此时 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转的度数．
答案解析收藏纠错 + 选题