湖南省长沙市浏阳市2023-2024学年上学期八年级期中质量...

更新时间：2023-12-28 浏览次数：33 类型：期中考试

一、选择题（在下列各题的四个选项中，只有一项是符合题意的。请在答题卡中涂填涂符合题意的选项。本大题共10个小题，每小题3分，共30分）

1. (2024八上·浏阳期中) 剪纸是我国传统的民间艺术，下列剪纸作品中，是轴对称图形的是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2023八上·兴宁期中) 小明和小红两位小朋友在做拼三角形的游戏，小明手上有两根木棒长分别为4cm和7cm ，小红手上有四根木棒，长度如下：2cm ， 3cm ， 8cm ， 12cm ，小明从小红手中选一根要能拼成一个三角形，小明应选长为（　　）的木棒．

A . 2 cm B . 3cm C . 8cm D . 12cm

答案解析收藏纠错 + 选题
3. (2024八上·浏阳期中) 如图，人字梯中间一般会设计一“拉杆”，以增加使用梯子时的安全性，这样设计蕴含的数学依据是（　　）

A . 两直线平行，内错角相等 B . 垂线段最短 C . 两点之间，线段最短 D . 三角形具有稳定性

答案解析收藏纠错 + 选题
4. (2024八上·浏阳期中) 如图，∠1＝40°，则∠C的度数为（　　）

A . 30° B . 40° C . 50° D . 60°

答案解析收藏纠错 + 选题
5. (2024八上·浏阳期中) 在如图所示的尺规作图中，与AD相等的线段是（　　）

A . 线段AC B . 线段BD C . 线段DC D . 线段DE

答案解析收藏纠错 + 选题
6. (2024八上·浏阳期中) 如图，∠AOB是一个任意角，在边OA ， OB上分别取OM＝ON ，移动角尺，使角尺两边相同的刻度分别与M ， N重合，过角尺顶点C的射线OC便是∠AOB的平分线OC ，作法用到的三角形全等的判定方法是（　　）

A . SAS B . SSS C . ASA D . HL

答案解析收藏纠错 + 选题
7. (2024八上·新会月考) 下列多边形中，对角线是5条的多边形是（）

A . 四边形 B . 五边形 C . 六边形 D . 七边形

答案解析收藏纠错 + 选题
8. (2024八上·浏阳期中) 如图，在五边形 $\text{[math]}$ 中， $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分别是 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的外角，则 $\text{[math]}$ 的度数为（）

A . 180° B . 210° C . 240° D . 270°

答案解析收藏纠错 + 选题
9. (2024八上·浏阳期中) 如图是两个全等三角形，图中的字母表示三角形的边长，则 $\text{[math]}$ 的度数是（）

A . 54° B . 56° C . 60° D . 66°

答案解析收藏纠错 + 选题
10. (2024八上·浏阳期中) 在如图的三角形纸片中，AB＝8cm ， BC＝6cm ， AC＝5cm ，沿过点B的直线折叠这个三角形，使点C落在AB上的点E处，折痕为BD ，则△AED的周长为（　　）

A . 5cm B . 6cm C . 7cm D . 8cm

答案解析收藏纠错 + 选题

二、填空题（本大题共6个小题，每小题3分，共18分）

11. (2024八上·浏阳期中) 点P（﹣4，1）关于x轴对称的点的坐标是

答案解析收藏纠错 + 选题
12. (2024八上·浏阳期中) 用一根长12cm的铁丝围成一个等边三角形，那么这个等边三角形的边长为 cm ．

答案解析收藏纠错 + 选题
13. (2024八上·广州期中) 如图，已知 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
14. (2024八上·浏阳期中) 如图所示，已知点B、C、F、E在同一条直线上 ， ∠1＝∠2，AF＝CD ，要使△ABF≌△DEC那么可以补充哪一个条件．（只填一个即可）

答案解析收藏纠错 + 选题
15. (2024八上·浏阳期中)
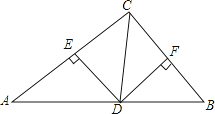
如图，在△ABC中，CD平分∠ACB交AB于点D，DE⊥AC交于点E，DF⊥BC于点F，且BC=4，DE=2，则△BCD的面积是．

答案解析收藏纠错 + 选题
16. (2024八上·浏阳期中) 如图所示，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，EF垂直平分BC ，交AC于点D ，交BC于点G ，点P为直线EF上一动点，则 $\text{[math]}$ 周长的最小值是．

答案解析收藏纠错 + 选题

三、解答题（本大题共9个小题，第17、18、19题每小题6分，第20、21题每小题6分，第22、23题每小题6分，第24、25题每小题6分，共72分。解答应写出必要的文字说明、证明过程或演算步骤）

17. (2024八上·浏阳期中) 计算：
1. （1） 8-|-5|+（-4）×（-3）；
2. （2） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
18. (2024八上·浏阳期中) 先化简，再求值：2（a²-2a+3）-3（a²+2a-1），其中a＝2．

答案解析收藏纠错 + 选题
19. (2024八上·浏阳期中) 如图，在平面直角坐标系xOy中，点A的坐标为（-4，4），点B的坐标为（-2，0），点C的坐标为（-1，2）．
1. （1）请面出△ABC关于y轴的对称图形△A₁B₁C₁；
2. （2）直接写出A₁ ， B₁ ， C₁三点的坐标；
3. （3）求△ABC的面积．
答案解析收藏纠错 + 选题
20. (2024八上·永定期末) 如图，∠1＝∠2，AB＝AE ， AC＝AD ．求证：BC＝ED ．

答案解析收藏纠错 + 选题
21. (2024八上·浏阳期中) 已知：如图，△ABC中，AB＝AC ， D为BC上一点，过点D作DE∥AB交AC于点E ．
1. （1）求证：∠C＝∠CDE ．
2. （2）若∠A＝60°，试判断△DEC的形状，并说明理由．
答案解析收藏纠错 + 选题
22. (2024八上·浏阳期中) 如图，在△ABC中，∠C＝90°，∠B＝30°，DE是AB的垂直平分线，垂足为点E ， DE交BC于点D ，连接AD ．
1. （1）求证：AD平分∠CAB；
2. （2）若CD＝3，求BD的长．
答案解析收藏纠错 + 选题
23. (2024八上·浏阳期中) 如图，PC平分∠APB ， CM⊥PA于点M ， CN⊥PB于点N ， D ， E分别是边PA和PB上的点，且CD＝CE ．求证：
1. （1） △CMD≌△CNE；
2. （2） ∠APB+∠DCE＝180°．
答案解析收藏纠错 + 选题
24. (2024八上·浏阳期中) 规定：如果一个三角形的三个角分别等于另一个三角形的三个角，那么称这两个三角形互为“等角三角形”．
从三角形（不是等腰三角形）一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形是“等角三角形”，我们把这条线段叫做这个三角形的“等角分割线”．
1. （1）如图1，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，请写出图中两对“等角三角形”；
2. （2）如图2，在 $\text{[math]}$ 中， $\text{[math]}$ 为 $\text{[math]}$ 的平分线， $\text{[math]}$ ， $\text{[math]}$ ．求证： $\text{[math]}$ 为 $\text{[math]}$ 的“等角分割线”；
3. （3）在 $\text{[math]}$ 中，若 $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的“等角分割线”，请求出所有可能的 $\text{[math]}$ 的度数．
答案解析收藏纠错 + 选题
25. (2024八上·浏阳期中) 在等边△ABC中，点D是边BC上一点．作射线AD ，点B关于射线AD的对称点为点E ．连接CE并延长，交射线AD于点F ．
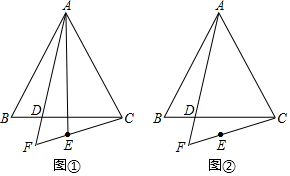
1. （1）如图①，连接AE ，
  ①AE与AC的数量关系是 ▲ ；
  ②设∠BAF＝a ，用a表示∠BCF的大小；
2. （2）如图②，用等式表示线段AF ， CF ， EF之间的数量关系，并证明．
答案解析收藏纠错 + 选题