吉林省松原市前郭县第三中学2023-2024学年八年级上学期...

更新时间：2024-03-21 浏览次数：40 类型：月考试卷

一、单项选择题（每小题2分，共12分）

1. (2023·陆河模拟) 剪纸文化是中国最古老的民间艺术之一，下列剪纸图案中，不是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2023八上·前郭尔罗斯月考) 下列运算正确的是（）

A . （a²）³=a⁵ ． B . （a²b）³=a6b³ ． C . a⁶÷a³=a² ． D . a²·a⁴=a⁸ ．

答案解析收藏纠错 + 选题
3. (2023八上·前郭尔罗斯月考) 如图，OB平分∠AOC，D，E，F分别是射线OA，射线OB，射线OC上的点，D，E，F与0点都不重合，连接ED， EF．若添加下列条件中的某一个，使△DOE≌△FOE．下列条件不一定成立的是（）

A . DE=FE． B . OD=OF． C . ∠OED=∠OEF． D . ∠ODE=∠OF．

答案解析收藏纠错 + 选题
4. (2023八上·前郭尔罗斯月考) 将9.5²变形正确的是（）

A . 9.5²=9²+0.5² ． B . 9.5²=（10+0.5）（10- 0.5）． C . 9.5²=10²-2×10×0.5+0.5² ． D . 9.5²=9²+9×0.5+0.5² ．

答案解析收藏纠错 + 选题
5. (2023八上·前郭尔罗斯月考) 如图分割的正方形，拼接成长方形方案中，可以验证（）

A . （a+b）²=a²+2ab+b² ． B . （a-b）²=a²-2ab+b² ． C . （a-b）²=（a+b）²-4ab． D . （a+b）（a-b）=a²-b² ．

答案解析收藏纠错 + 选题
6. 若k为任意整数，则（2k+3）²-4k²的值总能（）

A . 被2整除． B . 被3整除． C . 被5整除． D . 被7整除．

答案解析收藏纠错 + 选题

二、填空题（每小题3分，共24分）

7. (2023八上·前郭尔罗斯月考) 计算（-2）⁰的结果是

答案解析收藏纠错 + 选题
8. (2023七下·桂林期中) 若a^m=5，aⁿ=3，则a^m+n=.

答案解析收藏纠错 + 选题
9. (2023八上·前郭尔罗斯月考) 已知点P（-3，1），则点P关于x轴对称的点的坐标是

答案解析收藏纠错 + 选题
10. (2023八上·前郭尔罗斯月考) 计算：（6m²-3m）+ 3m=．

答案解析收藏纠错 + 选题
11. (2024·金华月考) 分解因式：m³-16m=

答案解析收藏纠错 + 选题
12. (2023八上·前郭尔罗斯月考) 已知x+y=1，xy=-3，则x²+y²=

答案解析收藏纠错 + 选题
13. (2023八上·前郭尔罗斯月考) 如图，长方形的长、宽分别为a，b，且a比b大3，面积为7，则a²b-ab²的值为

答案解析收藏纠错 + 选题
14. (2023八上·前郭尔罗斯月考) 如图，△ABC是等边三角形，直线l过顶点B，作点C关于直线l的对称点D，连接BD，AD，CD，若∠BAD=25°，则∠BCD的度数为

答案解析收藏纠错 + 选题

三、解答题（每小题5分，共20分）

15. (2023八上·前郭尔罗斯月考) 计算：x³·x⁴·x-（x²）⁴+（2x⁴）² ．

答案解析收藏纠错 + 选题
16. (2023八上·前郭尔罗斯月考) 计算：-3a·（a²-ab+2b²）．

答案解析收藏纠错 + 选题
17. (2023八上·前郭尔罗斯月考) 计算：（x+2）（x-2）-x（x+1）．

答案解析收藏纠错 + 选题
18. (2023八上·前郭尔罗斯月考) 因式分解：（4a+b）-（2a+b）² ．

答案解析收藏纠错 + 选题

四、解答题（每小题7分，共28分）

19. (2023八上·前郭尔罗斯月考) 已知代数式：（x-1）²+（x +y）（x-y）+y² ．
1. （1）化简这个代数式；
2. （2）若x²-x=4，求原代数式的值．
答案解析收藏纠错 + 选题
20. (2023八上·前郭尔罗斯月考) 如图，△ABC中，AB=AC，点D在BC边上，连接AD，若AD=BD，AC=DC，求∠DAC的度数．

答案解析收藏纠错 + 选题
21. (2023八上·前郭尔罗斯月考) 如图，△ABC中，AD是BC边上的中线，E，F为直线AD上的点，连接BE，CF，且BE∥CF．
1. （1）求证：△BDE≌△CDF；．
2. （2）若AE=13，AF=7，求DE的长．
答案解析收藏纠错 + 选题
22. (2023八上·前郭尔罗斯月考) 如何设计与制作风筝呢？请同学们阅读“勤学小组”的项目实施过程，帮助他们解决项目实施过程中遇到的问题。
项目主题：设计与制作风筝．
项目实施：
1. （1）任务一：了解风筝：“勤学小组”的同学查阅了有关风筝的历史，种类，结构，制作等方面的资料，同时还收集到如图的风筝图案，请你帮助他们从中选出不是轴对称图形的风筝图案
2. （2）任务二：设计风筝：设计风筝时主要进行风筝面与风筝骨架的设计．“勤学小组”的同学设计好了风筝面，接下来在正方形网格中进行风筝骨架的设计，请你帮助他们以直线l为对称轴画出风筝骨架的另一半．
3. （3）任务三：制作风筝：传统风筝的技艺概括起来四个字：扎、糊、绘、放，简称“四艺”．“勒学小组”的同学准备用竹条扎制如图所示的风筝骨架，已知AD⊥BC于点D， BD=CD，AB=60cm，则竹条AC的长为cm．
4. （4）任务四：放飞风筝：同学们拿着自己设计与制作的风筝进行了试飞，并根据试飞结果对风筝进行了修改完善．
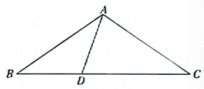
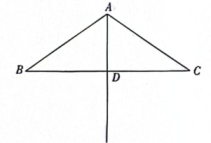
  项目反思：同学们对项目学习的整个过程进行反思，并编写了“简易风筝制作说明书”。请你写出一条在项目实施的过程中用到的数学知识
答案解析收藏纠错 + 选题

五、解答题（每小题8分，共16分）

23. (2023八上·前郭尔罗斯月考) 如图，在长方形ABCD中，点E在边AD上，将此长方形沿CE折叠，点D落在点F处，连接BF，B，F，E三点恰好在一直线上．
1. （1）求证：△BEC为等腰三角形；
2. （2）若AE=CD，直接写出∠ECF的度数．
答案解析收藏纠错 + 选题
24. (2023八上·前郭尔罗斯月考)
如图①，正方形ABCD的面积为1．
1. （1）如图②，延长AB到A₁ ，使A₁B=BA，延长BC到B₁ ，使B₁C=CB，则四边形AA₁B₁D的面积为
2. （2）如图③，延长AB到A₂ ，使A₂B=2BA，延长BC到B₂ ，使B₂C=2CB，则四边形AA₂B₂D的面积为
3. （3）延长AB到A_n ，使A_nB=nBA，延长BC到Bn，使B_nC=nCB，求四边形AA_nB_nD的面积（用含n的式子表示）
答案解析收藏纠错 + 选题

六、解答题（每小题10分，共20分）

25. (2023八上·前郭尔罗斯月考)
1. （1）分解下列因式，将结果直接写在横线上：
  x²-6x+9=
  25 x²+10x +1=
  4x²+12x+9=
2. （2）观察上述三个多项式的系数，有：
  （-6）²=4×1×9，
  10²=4×25×1，
  12²=4×4×9．
  于是小明猜测：若多项式ax²+bx +c（a>0）是完全平方式，那么系数a，b，c之间一定存在某种关系．请你用数学式子表示小明的猜测：；
3. （3）已知多项式（x-a）（x-b）-x（b-x）+2是一个完全平方式，求（a-2b）²的值．
答案解析收藏纠错 + 选题
26. (2023八上·前郭尔罗斯月考) 根据几何图形的面积关系可以说明数学等式，例如：（2a+b）（a+b）=2a²+3ab+b² ，可以用图①的面积关系来说明，由此我们识可以得到（2a+b）（a+b）-（2a²+b²）=3ab．
1. （1）根据图②的面积关系可得：（2a+b）（a+2b）-（2a²+2b²）=；
2. （2）有若干张如图③的三种纸片，A种纸片是边长为a的正方形，B种纸片是边长为b的正方形，C种纸片是长为a，宽为b的长方形．并用这些纸片无缝隙无重叠地拼成了图④，图⑤，图⑥的图形，图④，图⑤，图⑥中的阴影部分面积分别记为S₁ ， S₂ ， S₃；
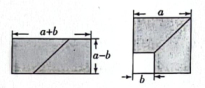
  ①S₁= ▲ ， S₂= ▲ ， S₃= ▲ （用含a， b的代数式表示）；
  ②若3S₂-S₁=108，S₃=9，求图⑥中大正方形的面积．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

吉林省松原市前郭县第三中学2023-2024学年八年级上学期...

副标题：

*注意事项：

吉林省松原市前郭县第三中学2023-2024学年八年级上学期...

试题分析

总体分析

题量分析

难度分析

知识点分析