山东省济南市平阴县2023-2024学年九年级上学期期中数学...

更新时间：2024-01-09 浏览次数：40 类型：期中考试

一、选择题（共10小题，每小题4分，共40分）

1. (2023九上·平阴期中) 方程x²﹣2022x﹣2023＝0中的一次项系数是（　　）

A . 2022x B . ﹣2022x C . 2022 D . ﹣2022

答案解析收藏纠错 + 选题
2. (2024·长沙模拟) 如图是由一个长方体和一个圆柱组成的几何体，它的俯视图是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2023九上·平阴期中) x²﹣10x﹣1＝0，变形正确的是（　　）

A . （x﹣5）²＝26 B . （x+5）²＝26 C . （x﹣5）²＝24 D . （x+5）²＝24

答案解析收藏纠错 + 选题
4. (2024八下·博山期末) 若 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . 6 B . $\text{[math]}$ C . 1 D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. 已知蓄电池的电压U为定值，使用蓄电池时，电流I（单位：A)与电阻R（单位：Ω）是反比例函数关系（ $\text{[math]}$ )．下列反映电流I与电阻R之间函数关系的图象大致是（）

A . B . C . D .

答案解析收藏纠错 + 选题
6. (2023九上·平阴期中) 若点C是线段AB的黄金分割点，AB＝8cm ， AC＞BC ，则AC等于（　　）

A . $\text{[math]}$ cm B . $\text{[math]}$ cm C . $\text{[math]}$ cm D . $\text{[math]}$ cm

答案解析收藏纠错 + 选题
7. (2023九上·平阴期中) 若点A（﹣2，y₁），B（2，y₂），C（3，y₃）都在反比例函数 $\text{[math]}$ 的图象上，则y₁ ， y₂ ， y₃的大小关系是（）

A . y₂＜y₃＜y₁ B . y₃＜y₂＜y₁ C . y₃＜y₁＜y₂ D . y₁＜y₂＜y₃

答案解析收藏纠错 + 选题
8. (2023九上·平阴期中) 如图，下列不能判定 $\text{[math]}$ 与 $\text{[math]}$ 相似的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2023九上·平阴期中) 反比例函数 $\text{[math]}$ 和一次函数y＝kx﹣k在同一平面直角坐标系中的大致图象是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
10. (2024九下·绥棱模拟) 皮克定理是格点几何学中的一个重要定理，它揭示了以格点为顶点的多边形的面积 $\text{[math]}$ ，其中 $\text{[math]}$ 分别表示这个多边形内部与边界上的格点个数．在平面直角坐标系中，横、纵坐标都是整数的点为格点．已知 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 内部的格点个数是（）

A . 266 B . 270 C . 271 D . 285

答案解析收藏纠错 + 选题

二、填空题（共6个小题，每小题4分，共24分）

11. (2023九上·平阴期中) 在不透明的袋子里装有红球、黄球共20个，这些球除颜色外都相同．小明通过多次实验发现，摸出红球的频率稳定在0.8左右，则袋子中红球的个数最有可能是个．

答案解析收藏纠错 + 选题
12. (2023九上·平阴期中) 已知一元二次方程x²﹣3x+k＝0的两个实数根为a ， b ，若ab+2a+2b＝1，则实数k＝．

答案解析收藏纠错 + 选题
13. (2023九上·平阴期中) 如图所示，D、E分别是△ABC的边AB、AC上的点，DE∥BC ，并且AD：BD＝2：1，那么S_△_ADE和S_△_ABC的比为．

答案解析收藏纠错 + 选题
14. (2023九上·平阴期中) 如图，在长为100m ，宽为50m的矩形空地上修筑四条宽度相等的小路，若余下的部分全部种上花卉，且花圃的面积是3600m² ，则小路的宽是 m ．

答案解析收藏纠错 + 选题
15. (2023九上·平阴期中) 如图，正方形四个顶点分别位于两个反比例函数 $\text{[math]}$ 和 $\text{[math]}$ 的图象的四个分支上，则n的值＝．

答案解析收藏纠错 + 选题
16. (2023九上·平阴期中) 一张直角三角形纸片ABC，∠ACB=90°，AB=10，AC=6，点D为BC边上的任一点，沿过点D的直线折叠，使直角顶点C落在斜边AB上的点E处，当△BDE是直角三角形时，则CD的长为.

答案解析收藏纠错 + 选题

三、解答题（共10个小题，共86分，解答应写出文字说明，证明过程或演算步骤）

17. (2023九上·平阴期中) 解下列方程：
1. （1） x²﹣4x﹣1＝0；
2. （2）（x+3）（x﹣3）＝3（x+3）．
答案解析收藏纠错 + 选题
18. (2023九上·平阴期中) 如图，在△ABC和△DEC中，∠A＝∠D ， ∠BCE＝∠ACD ．求证：△ABC∽△DEC ．

答案解析收藏纠错 + 选题
19. (2023九上·平阴期中) 如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（﹣4，3），B（﹣3，1），C（﹣1，3），请按下列要求画图：以点A为位似中心，在网格中画出△ABC的位似图形△AB₁C₁ ，使△AB₁C₁与△ABC的相似比为2：1；并写出点B₁的坐标．

答案解析收藏纠错 + 选题
20. (2023九上·平阴期中) 如图，一次函数y＝mx+n的图象与y轴交于点A ，与反比例函数y＝ $\text{[math]}$ （x＞0）的图象交于点B（3，a）．
1. （1）求点B的坐标；
2. （2）用m的代数式表示n；
3. （3）当△OAB的面积为9时，求一次函数y＝mx+n的表达式．
答案解析收藏纠错 + 选题

21. (2023九上·平阴期中) 首届楚文化节在荆州举办前，主办方为使参与服务的志愿者队伍整齐，随机抽取了部分志愿者，对其身高进行调查，将身高（单位：cm）数据分A，B，C，D，E五组制成了如下的统计图表（不完整）．

组别	身高分组	人数
A	155≤x＜160	3
B	160≤x＜165	2
C	165≤x＜170	m
D	170≤x＜175	5
E	175≤x＜180	4

根据以上信息回答：

（1）这次被调查身高的志愿者有人，表中的 $\text{[math]}$ ，扇形统计图中α的度数是；
（2）若E组的4人中，男女各有2人，以抽签方式从中随机抽取两人担任组长．请列表或画树状图，求刚好抽中两名女志愿者的概率．

答案解析收藏纠错 + 选题

22. (2023九上·平阴期中) 某扶贫单位为了提高贫困户的经济收入，购买了39m的铁栅栏，准备用这些铁栅栏为贫困户靠墙（墙长15m）围建一个中间带有铁栅栏的矩形养鸡场（如图所示）．
1. （1）若要建的矩形养鸡场面积为120m² ，求鸡场的长AB和宽BC；
2. （2）该扶贫单位想要建一个130m²的矩形养鸡场，这一想法能实现吗？请说明理由．
答案解析收藏纠错 + 选题
23. (2023九上·平阴期中) 如图，在正方形 $\text{[math]}$ 中， $\text{[math]}$ 为边 $\text{[math]}$ 的中点，点 $\text{[math]}$ 在边 $\text{[math]}$ 上，且 $\text{[math]}$ ，延长 $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ．
1. （1）求证：△ $\text{[math]}$ ∽△ $\text{[math]}$ ．
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
24. (2023九上·平阴期中) 一次函数y＝﹣x+m与反比例函数 $\text{[math]}$ 的图象交于A ， B两点，点A的坐标为（1，2）．
1. （1）求一次函数和反比例函数的表达式；
2. （2）求△OAB的面积；
3. （3）过动点T（t ， 0）作x轴的垂线l ， l与一次函数y＝﹣x+m和反比例函数 $\text{[math]}$ 的图象分别交于M ， N两点，当M在N的上方时，请直接写出t的取值范围．
答案解析收藏纠错 + 选题
25. (2023九上·平阴期中) 阅读下列材料：利用完全平方公式，将多项式x²+bx+c变形为（x+m）²+n的形式，然后由（x+m）²≥0就可求出多项式x²+bx+c的最小值．
例题：求多项式x²﹣4x+5的最小值．
解：x²﹣4x+5＝x²﹣4x+4+1＝（x﹣2）²+1，
因为（x﹣2）²≥0，所以（x﹣2）²+1≥1．
当x＝2时，（x﹣2）²+1＝1．因此（x﹣2）²+1有最小值，最小值为1，即x²﹣4x+5的最小值为1．
通过阅读，理解材料的解题思路，请解决以下问题：
1. （1）【理解探究】
  已知代数式A＝x²+10x+20，则A的最小值为；
2. （2）【类比应用】
  张大爷家有甲、乙两块长方形菜地，已知甲菜地的两边长分别是（3a+2）米、（2a+5）米，乙菜地的两边长分别是5a米、（a+5）米，试比较这两块菜地的面积S_甲和S_乙的大小，并说明理由；
3. （3）【拓展升华】
  如图，△ABC中，∠C＝90°，AC＝5cm ， BC＝10cm ，点M、N分别是线段AC和BC上的动点，点M从A点出发以1cm/s的速度向C点运动；同时点N从C点出发以2cm/s的速度向B点运动，当其中一点到达终点时，两点同时停止运动，设运动的时间为t ，则当t的值为多少时，△MCN的面积最大，最大值为多少？
答案解析收藏纠错 + 选题
26. (2023九上·平阴期中) 【问题呈现】
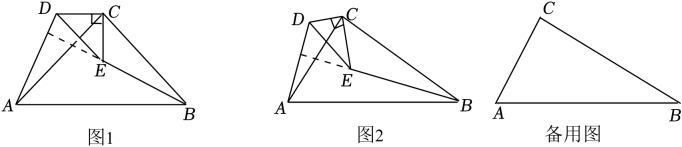
△CAB和△CDE都是直角三角形，∠ACB＝∠DCE＝90°，CB＝mCA ， CE＝mCD ，连接AD ， BE ，探究AD ， BE的位置关系．
【问题探究】
1. （1）如图1，当m＝1时，直接写出AD ， BE的位置关系：．
2. （2）如图2，当m≠1时，（1）中的结论是否成立？若成立，给出证明；若不成立，说明理由．
3. （3）【拓展应用】当 $\text{[math]}$ ， $\text{[math]}$ ， DE＝4时，将△CDE绕点C旋转，使A ， D ， E三点恰好在同一直线上，求BE的长．
答案解析收藏纠错 + 选题