河北省石家庄市四十一中2023-2024学年八年级上学期期中...

更新时间：2024-01-31 浏览次数：39 类型：期中考试

一、选择题（本大题共16个小题，1-6小题每小题3分，7-16小题每小题3分，共38分.）

1. (2024八上·宝安月考) 下列四个实数中，属于无理数的是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . 3.1415926 D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023八上·河北期中) 16的算术平方根是（）

A . 16 B . 4 C . ﹣4 D . ±4

答案解析收藏纠错 + 选题
3. (2023八上·河北期中) 如图的两个三角形全等，则 $\text{[math]}$ 的度数为（）

A . 50° B . 58° C . 60° D . 62°

答案解析收藏纠错 + 选题
4. (2023八上·河北期中) 若代数式 $\text{[math]}$ 有意义，则实数x的取值范围是（　　）

A . x≥﹣2 B . x＞﹣2 C . x≤﹣2 D . x＜﹣2

答案解析收藏纠错 + 选题
5. (2023八上·河北期中) 下列计算正确的是（　　）

A . $\text{[math]}$ ＝±3 B . $\text{[math]}$ C . $\text{[math]}$ ＝﹣3 D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023八上·河北期中) 近似数1.80是精确到（　　）

A . 十位 B . 百位 C . 十分位 D . 百分位

答案解析收藏纠错 + 选题
7. (2023八上·河北期中) 用直尺和圆规作一个角等于已知角的示意图如下，则要说明∠AOB＝∠A′O′B′，需要证明△COD和△C'O'D'，则这两个三角形全等的依据是（　　）

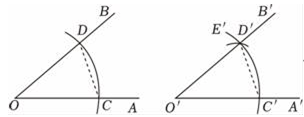
A . SAS B . AAS C . SSS D . ASA

答案解析收藏纠错 + 选题
8. (2023八上·河北期中) 若分式 $\text{[math]}$ 的值为零，则x的值是（　　）

A . ﹣2 B . 2或﹣2 C . 2 D . 4

答案解析收藏纠错 + 选题
9. (2023八上·河北期中) 如图，在△ABC和△DEF中，点A、E、B、D在同一条直线上，AC∥DF ， AC＝DF ，只添加一个条件，不能判断△ABC≌△DEF的是（　　）

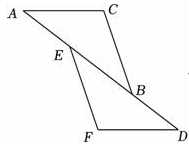
A . AE＝DB B . ∠C＝∠F C . BC＝EF D . ∠ABC＝∠DEF

答案解析收藏纠错 + 选题
10. (2023八上·河北期中) 如图是一个“数值转换机”，按下面的运算过程输入一个数x ，若输入的数x＝4，则输出的结果y为（　　）

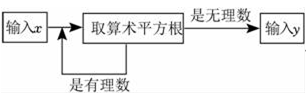
A . 2 B . ﹣2 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2023八上·河北期中) 下列命题的逆命题为真命题的是（　　）

A . 对顶角相等 B . 若a＞b ，则a²＞b² C . 全等三角形的面积相等 D . 两直线平行，同位角相等

答案解析收藏纠错 + 选题
12. (2023八上·河北期中) 老师设计了接力游戏，用合作的方式完成分式化简，规则是：每人只能看到前一人给的式子，并进行一步计算，再将结果传递给下一人，最后完成化简．过程如图所示：
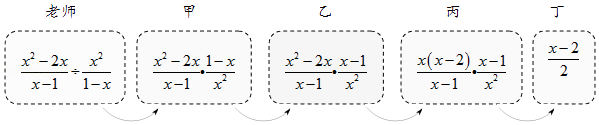
接力中，自己负责的一步出现错误的是（）

A . 只有乙 B . 甲和丁 C . 乙和丙 D . 乙和丁

答案解析收藏纠错 + 选题
13. (2023八上·河北期中) 如图，面积为6的正方形ABCD的顶点A在数轴上，且表示的数为﹣1，若点E在数轴上，（点E在点A的右侧）且AB＝AE ，则点E所表示的数为（　　）

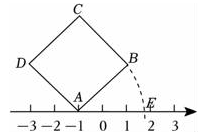
A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
14. (2023八上·河北期中) 下列说法正确的个数是（　　）
①数轴上的点与有理数是——对应的；
② $\text{[math]}$ 的倒数是 $\text{[math]}$ ；
③ $\text{[math]}$ 是最简二次根式；
④一个实数不是正实数就是负实数；
⑤绝对值小于 $\text{[math]}$ 的整数共有5个．

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
15. (2024八下·农安期末) 为了缅怀革命先烈，传承红色精神，青海省某学校八年级师生在清明节期间前往距离学校 $\text{[math]}$ 的烈士陵园扫墓.一部分师生骑自行车先走，过了 $\text{[math]}$ 后，其余师生乘汽车出发，结果他们同时到达；已知汽车的速度是骑车师生速度的2倍，设骑车师生的速度为 $\text{[math]}$ .根据题意，下列方程正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
16. (2023八上·河北期中) 如图，在Rt $\text{[math]}$ 和Rt $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， BE与AC相交于点M，与CF相交于点D，AB与CF相交于点N， $\text{[math]}$ ．有下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ ≌ $\text{[math]}$ ．其中正确结论的个数是（）．

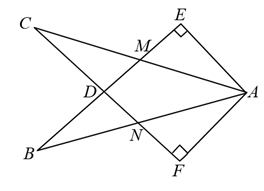
A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题（本大题有3个小题，每小题3分，共9分.）

17. (2023八上·河北期中) 比较大小： $\text{[math]}$ 3．

答案解析收藏纠错 + 选题
18. (2023八上·河北期中) 若关于x的分式方程 $\text{[math]}$ 有增根，则m＝．

答案解析收藏纠错 + 选题
19. (2023八上·河北期中) 如图，在△ABC中，∠ACB＝90°，AC＝6，BC＝8，点C在直线l上．点P从点A出发，在三角形边上沿A→C→B的路线向终点B运动；点Q从B点出发，在三角形边上沿B→C→A的路线向终点A运动．点P和Q分别以1单位/秒和2单位秒的速度同时开始运动，在运动过程中，若有一点先到达终点时，该点停止运动，另一个点也停止运动．分别过点P和Q作PE⊥l于点E ， QF⊥l于点F ，当△PEC与△CFQ全等时，点P的运动时间为秒．

答案解析收藏纠错 + 选题

三、解答题（本大题有7个小题，共73分.解答应写出文字说明、证明过程或演算步骤）

20. (2023八上·河北期中) 解下列方程：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
21. (2024八上·凉州期末) 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
22. (2023八上·河北期中) 计算：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ ；
3. （3） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
23. (2023八上·河北期中) 如图， $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 边上的中线， $\text{[math]}$ ， $\text{[math]}$ 为直线 $\text{[math]}$ 上的点，连接 $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，试求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
24. (2024八上·广州期末) 某商场计划购进一批篮球和足球，其中篮球的单价比足球的单价多30元，已知用360元购进的足球和用480元购进的篮球数量相等．
1. （1）篮球和足球的单价各是多少元？
2. （2）若篮球售价为每个150元，足球售价为每个110元，商场售出足球的数量比篮球数量的三分之一还多10个，且获利超过1300元，问篮球最少要卖多少个？
答案解析收藏纠错 + 选题
25. (2023八上·河北期中) 【综合与实践】如图，把两个面积均为18cm²的小正方形纸片分别沿对角线裁剪后拼成一个大的正方形纸片．
1. （1）大正方形纸片的边长为 cm；
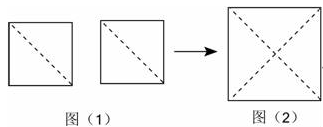
2. （2）若沿此大正方形纸片边的方向裁剪出一个长方形纸片，能否使裁剪出的长方形纸片的长宽之比为4：3，且面积为24cm²？若能，求剪出的长方形纸片的长和宽；若不能，试说明理由．
答案解析收藏纠错 + 选题
26. (2023八上·河北期中) 如图1，△ABC中，AB＝BC＝CA ， ∠A＝∠ABC＝∠ACB＝60°，在△ABC的顶点A ， C处各有一只小蚂蚁，它们同时出发，分别以相同速度由A向B和由C向A爬行，经过t（s）后，它们分别爬行到了D ， E处，连接DC ， BE ， DC与BE相交于点F ．
1. （1）求证：△ACD≌△CBE；
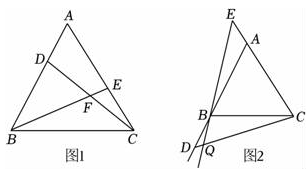
2. （2）小蚂蚁在爬行过程中，∠BFC的大小会变化吗？若变化，请说明理由；若不变，求∠BFC的度数；
3. （3）如图2，当小蚂蚁分别爬行到线段AB ， CA的延长线上的D ， E处时，若EB的延长线与CD交于点Q ，其他条件不变，请直接写出∠CQE的度数．
答案解析收藏纠错 + 选题