 B .
B .  C .
C .  D .
D . 

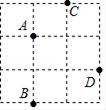



已知:如图,点A,B,C,D在同一条直线上,AB=CD,∠E=∠F,EC∥FB.

求证:EA=FD.
证明:∵AB=CD(已知),
∴AB+BC=CD+BC.
∴AC=DB.
∵EC∥FB(已知),
∴∠1=∠2( ▲ ).
在△AEC和△DFB中,
,
∴△AEC≌△DFB( ▲ ).
∴EA=FD( ▲ ).
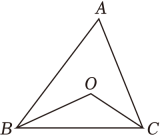
已知:如图,AC=AD,∠C=∠D,∠1=∠2.

求证:AB=AE.
证明:∠1=∠2,
∴∠1+∠BAD=∠2+∠BAD.
∴∠ ▲ =∠EAD.
在△ABC和△AED中,
.
∴ ▲ .
∴AB=AE.
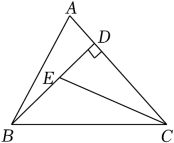
已知:如图,四边形ABCD中,AB=AD,∠B=∠D=90°.

求证:AC平分∠BAD.
证明:∵∠B=∠D=90°.
∴在Rt△ABC和Rt△ADC中,
,
∴Rt△ABC≌Rt△ADC( ▲ ).
∴∠ ▲ =∠ ▲ .
∴AC平分∠BAD.
已知:如图,在△ABC中,AB=AC,AD是BC边上的中线,CE⊥AB于点E.

求证:∠CAD=∠BCE.
证明:∵AB=AC,
∴∠B=∠ ▲ ,
∵AD是BC边上的中线,
∴AD ▲ BC(三线合一).
∴∠ADC=90°.
∴∠CAD+∠ACB=90°,
∵CE⊥AB,
∴∠BEC=90°.
∵∠ ▲ +∠B=90°,
∴∠CAD=∠BCE.
如图,△ABC中,AD⊥BC于点D,AD=BD,∠C=65°,求∠BAC的度数.


①a的取值范围是 ;
②当△ABC是等腰三角形时,按上述规律对应的等式是 .

