一、选择题(共12小题,每小题3分,共36分.在每小题给出的四个选项中只有一项是符合要求的,用2B铅笔把答题卡上对应题目的答案标号涂黑.)
-
-
A . 2cm,4cm,6cm
B . 8cm,6cm,4cm
C . 14cm,6cm,7cm
D . 2cm,3cm,6cm
-
-
4.
(2023八上·邕宁期中)
某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事方法是( )
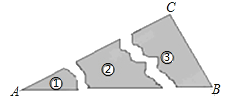
A . 带①去
B . 带②去
C . 带③去
D . ①②③都带去
-
A . 4
B .  C .
C .  D . 16
D . 16
-
-
A . 55°
B . 40°
C . 55°或40°
D . 20°或40°
-
A . AAS
B . SSS
C . ASA
D . SAS
-
A . ∠B=∠C
B . AD=2AB
C . ∠BAD=∠CAD
D . AD⊥BC
-
10.
(2023八上·邕宁期中)
如图,是由三个边长相等的正方形拼成的一个长方形,那么图中两个三角形的面积S
1和S
2的大小关系是( )

A . S1>S2
B . S1<S2
C . S1=S2
D . 不确定
-
11.
(2023八上·邕宁期中)
如图,在△ABC中,OB,OC分别是∠ABC和∠ACB的角平分线,过点O的直线MN∥BC,交AB,AC于M、N.若MN=6cm,则BM+CN=( )cm.

A . 6
B . 7
C . 8
D . 9
-
12.
(2023八上·邕宁期中)
如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,下列说法:①AE平分∠DAB,②点E到AD的距离等于CE,③AE=DE,④AD=AB+CD.其中正确的有( )

A . 3个
B . 2个
C . 1个
D . 4个
二、填空题(本大题共6小题,每小题2分,共12分.)
三、解答题(本大题共8小题,共72分.解答应写出文字说明、证明过程或演算步骤.)
-
-
-
(1)
在图中画出△ABC关于y轴的对称图形△A1B1C1 , 并分别写出对应点A1、B1、C1的坐标.
-
-
-
-
(1)
尺规作图:求作∠ABC的平分线BD,交AC于点D;
-
-
-
24.
(2023八上·邕宁期中)
如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是点E、F,BE=CF,求证:AD平分∠BAC.

-
-
26.
(2023八上·邕宁期中)
综合实践
在学习全等三角形的知识时,数学兴趣小组发现这样一个模型:它是由两个共顶点且顶角相等的等腰三角形构成的,在相对位置变化的同时,适中存在一对全等三角形,兴趣小组成员经过研讨给出定义:如果两个等腰三角形的顶角相等,且顶角的顶点互相重合,则称此图形为“手拉手全等模型”.因为顶点相连的四条边,可以形象地看作两双手,所以通常称为“手拉手模型”,如图1,△ABC与△ADE都是等腰三角形,其中∠BAC=∠DAE,则△ABD≌△ACE(SAS).

-
(1)
[初步把握]如图2,△ABC与△ADE都是等腰三角形,AB=AC,且∠BAC=∠DAE,则有 ≌.
-
(2)
[深入研究]如图3,已知△ABC,以AB、AC为边分别向外作等边△ABD和等边△ACE,并连接BE、CD,求证:BE=CD.
-
(3)
[拓展延伸]如图4,在两个等腰直角三角形△ABC和△ADE中,AB=AC,AE=AD,∠BAC=∠DAE=90°,连接BD,CE,交于点P,请判断BD和CE的关系,并说明理由.
 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D .