一、选择题(本大题10个小题,每小题4分,共40分)在每个小题的下面,都给出了代号为A、B、C、D的四个答案,其中只有一个是正确的,请将答题卡上题号右侧正确答案所对应的方框涂黑。
-
A . 3
B . -3
C . ±3
D . 81
-
-
-
-
A . 同旁内角互补
B . 对顶角相等
C . 两点确定一条直线
D . 等腰三角形两底角相等
-
-
A . ED∥AB
B . EB=FC
C . DF=AC
D . 
-
A . SSS
B . SAS
C . ASA
D . AAS
-
A . 6
B . 8
C . 11
D . 18
-
10.
(2023八上·重庆市期中)
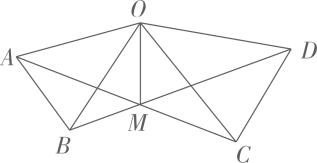
如图,在

和

中,

,

,

,

.连接

、

交于点M,连接

.下列结论:
①  ;②
;②  ;③
;③  平分
平分  ;④
;④  平分
平分 
其中正确的结论个数有( )个.
A . 4
B . 3
C . 2
D . 1
二、填空题(本大题8个小题,每小题4分,共32分)请将每小题的答案直接填在答题卡中对应的横线上。
-
-
-
-
-
15.
(2023八上·重庆市期中)
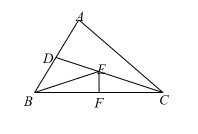
如图,在△ABC中,CD平分∠ACB,BC的垂直平分线交CD于点E,交BC于点F,连结BE.若∠A=60°,∠ABE=42°,则∠ACB的度数为
.
-
-
17.
(2023八上·重庆市期中)
观察下列一组图形,其中,第1个图形共有5条线段,第2个图形共有8条线段,…,按此规律,则第6个图形中线段的条数是
.

-
18.
(2023八上·重庆市期中)
一个数的数字排列完全颠倒过来就变成另一个数,简单地说就是顺序相反的两个数,我们把这样的一对数互称为“反序数”,如:123的反序数是321,4056的反序数是6504。根据以上阅读材料,若一个两位数与其反序数之和是一个整数的平方,求满足上述条件的所有两位数的和
.
三、解答题(本大题8个小题,第19题8分,其余每小题各10分,共78分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上。
-
-
(1)

-
(2)

-
-
(1)
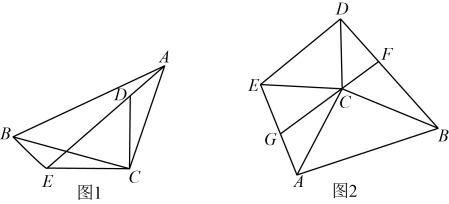
尺规作图:过点C作射线CF平分∠DCE交DE于点F(保留作图痕迹,不写做法)
-
(2)
在第(1)问的条件下,试探索CF与DE的位置关系,并说明理由:
证明:∵AD∥BE
∴∠A= ▲
在 和
和 中,
中,
∴ ( )
( )
∴CD=CE
∵CF平分∠DCE
∴ ▲
-
-
-
(1)
大学城第三中学校为学生军训调配备如图(1)所示的折叠凳,这样设计的折叠凳坐着舒适、稳定.这种设计所运用的数学原理是.
-
(2)
图(2)是折叠凳撑开后的侧面示意图.(木条等材科宽度忽略不计),其中凳腿AB和CD的长度相等,交点O是它们的中点,为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为38cm,则由以上信息可推得CB的长度是多少?请说明理由.
-
-
(1)
已知:

, 求

的值.
-
(2)
已知:

, 求

的值.
-
-
(1)

的整数部分是
,小数部分是
;
-
(2)
10+

也是夹在两个整数之间的,可以表示为

, 则

;
-
(3)
若

, 其中

是整数,且0<y<1,求:

的相反数.
-
25.
(2023八上·重庆市期中)
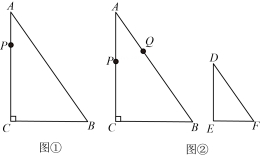
如图①,在Rt△ABC中,∠C=90°,BC=9cm,AC=12cm,AB=15cm,现有一动点P,从点A出发,沿着三角形的边AC→CB→BA运动,回到点A停止,速度为3cm/s,设运动时间为t秒:
-
(1)
如图①,当t =时,△APC的面积等于△ABC面积的一半;
-
(2)
如图②,在△DEF中,∠E=90°,DE=4cm,DF=5cm,∠D=∠A.在△ABC的边上,若另外有一个动点Q,与点P同时从点A出发,沿着边AB→BC→CA运动,回到点A停止.在两点运动过程中的某一时刻,恰好△APQ≌△DEF,求点Q的运动速度.
-
-
(1)
如图1,当点A旋转到ED的延长线时,求∠AEB的度数;
-
(2)
当Rt△ABC旋转到如图2所示的位置时,过点C作BD的垂线交BD于点F,交AE于点G,求证:BD=2CG.


和
中,
( )
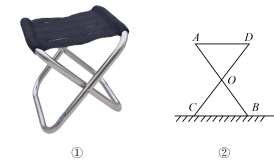
等,而常用“……”或者“≈”的表示方法都不够百分百准确,于是小刚用
来表示
的小数部分,你同意小刚的表示方法吗?事实上,小刚的表示方法是有道理的,因为
的整数部分是1,将这个数减去其整数部分,差就是小数部分,又例如:因为
, 即2<
<3,所以
的整数部分为2,小数部分为
, 也就是说,任何一个无理数,都可以夹在两个相邻的整数之间。根据上述信息,请回答下列问题: