贵州省从江县贯洞中学2023-2024学年七年级上学期数学期...

更新时间：2024-02-21 浏览次数：20 类型：期中考试

一、选择题:以下每小题均有A,B,C,D四个选项,其中只有一个选项正确,每小题3分,共36分.

1. (2023七上·龙川期末) 直线、线段、射线的位置如图所示，下图中能相交的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2023七上·从江期中) 在下列四个图形中，能用∠1，∠AOB，∠O三种方法表示同一个角的图形是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2023七上·从江期中) 下列关于作图的语句中叙述正确的是（）

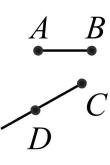
A . 画直线AB=10 cm B . 画射线OB=10 cm C . 已知A，B，C三点，过这三点画一条直线 D . 延长线段AB到点C，使BC=AB

答案解析收藏纠错 + 选题
4. (2023七上·从江期中) 从一个n边形的同一个顶点出发，分别连接这个顶点与其余各顶点，若把这个多边形分割成6个三角形，则n的值是（）

A . 6 B . 7 C . 8 D . 9

答案解析收藏纠错 + 选题
5. (2023七上·从江期中) 若∠A=30°18′，∠B=30°15′30″，∠C=30.25°，则这三个角的大小关系正确的是（）

A . ∠C>∠A>∠B B . ∠C>∠B>∠A C . ∠A>∠C>∠B D . ∠A>∠B>∠C

答案解析收藏纠错 + 选题
6. (2023七上·从江期中) 在下列生活、生产现象中，可以用基本事实“两点确定一条直线”来解释的是（）
①用两颗钉子就可以把木条固定在墙上；②把笔尖看成一个点，当这个点运动时便得到一条线；③把弯曲的公路改直，就能缩短路程；④植树时，只要栽下两棵树，就可以把同一行树栽在同一条直线上.

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023七上·从江期中) 如图所示，CB=4 cm，DB=7 cm，点D为AC的中点，则AB的长为（）

A . 7 cm B . 8 cm C . 9 cm D . 10 cm

答案解析收藏纠错 + 选题
8. (2023七上·从江期中) 一艘货轮O在航行过程中，发现灯塔A在它的北偏东65°方向上，同时发现货轮B在它的南偏东35°方向上，则∠AOB的度数为（）

A . 30° B . 50° C . 80° D . 100°

答案解析收藏纠错 + 选题
9. (2023七上·从江期中) 如图所示，直线AB，CD相交于点O，射线OM平分∠AOC，∠MON是直角.若∠AOM=35°，则∠CON的度数为（）

A . 35° B . 45° C . 55° D . 65°

答案解析收藏纠错 + 选题
10. (2023七上·从江期中) 如图所示，工作流程线上A，B，C，D处各有一名工人，且AB=BC=CD=1，现在工作流程线上安放一个工具箱，使4个人到工具箱的距离之和为最短，则工具箱安放的位置（）

A . 线段BC的任意一点处 B . 只能是A或D处 C . 只能是线段BC的中点E处 D . 线段AB或CD内的任意一点处

答案解析收藏纠错 + 选题
11. (2023七上·从江期中) 平面内有7条直线，这7条直线两两相交，最多可以得到a个交点，最少可以得到b个交点，则a+b的值是（）

A . 16 B . 22 C . 20 D . 18

答案解析收藏纠错 + 选题
12. (2023七上·从江期中) 如图所示，在方格纸中，点A，B，C，D，E，F，H，K中，在同一直线上的三个点有（）

A . 3组 B . 4组 C . 5组 D . 6组

答案解析收藏纠错 + 选题

二、填空题:每小题4分,共16分.

13. (2023七上·从江期中) 从十二边形的一个顶点作对角线，把这个十二边形分成个三角形.

答案解析收藏纠错 + 选题
14. (2023七上·从江期中) 一个圆被分成四个扇形，若各个扇形的面积之比为4∶2∶1∶3，则最小的扇形的圆心角的度数为.

答案解析收藏纠错 + 选题
15. (2023七上·从江期中) 3时30分时，时针与分针的夹角的度数是.

答案解析收藏纠错 + 选题
16. (2023七上·从江期中) 已知线段AB=8 cm，在直线AB上画线段BC，使它等于3 cm，则线段AC的长度为cm.

答案解析收藏纠错 + 选题

三、解答题:本大题9小题,共98分.解答应写出必要的文字说明、证明过程或演算步骤.

17. (2023七上·从江期中) 计算：
1. （1） 23°53′×3+107°43′÷5；
2. （2） 61°39′-22°5′32″.
答案解析收藏纠错 + 选题
18. (2023七上·从江期中) 已知平面上有四个村庄，用四个点A，B，C，D表示.
$\text{[math]}$ 连接AB；
$\text{[math]}$ 作射线AD；
$\text{[math]}$ 作直线BC与射线AD交于点E；
$\text{[math]}$ 若要建一供电所M，向四个村庄供电，要使所用电线最短，则供电所M应建在何处?请画出点M的位置并说明理由.

答案解析收藏纠错 + 选题
19. (2023七上·从江期中) 如图所示，已知线段AB.
1. （1）请用尺规按要求作图：延长线段AB至点C，使得BC=2AB(不写作法，保留作图痕迹)；
2. （2）若AB=3 cm，求线段AC的长.
答案解析收藏纠错 + 选题
20. (2023七上·从江期中) 如图所示，∠AOB是平角，∠BOC=36°，OD平分∠AOC，∠DOE=90°，求∠AOE的度数.

答案解析收藏纠错 + 选题
21. (2023七上·从江期中) 如图所示，一根5 m长的绳子，一端拴在90°的围墙墙角的柱子上，另一端拴着一只小羊(羊只能在草地上活动)，求小羊在草地上可活动区域的面积(结果保留π).

答案解析收藏纠错 + 选题
22. (2023七上·从江期中) 如图所示，已知轮船A在灯塔P的北偏东30°方向上，轮船B在灯塔P的南偏东70°方向上，轮船C在∠APB的平分线上.
1. （1）求∠APB的度数.
2. （2）轮船C在灯塔P的北偏东多少度方向上?
答案解析收藏纠错 + 选题
23. (2023七上·从江期中) 点P是线段AB上的一点，点M，N分别是线段AP，PB的中点.
1. （1）如图(1)所示，若点P是线段AB的中点，且MP=4 cm，求线段AB
  的长.
2. （2）如图(2)所示，若点P是线段AB上的任一点，且AB=12 cm，求线段MN的长.
3. （3）小明由(1)(2)猜想到，若点P是直线AB上的任意一点，且AB=12 cm，线段MN的长与(2)中结果一样，你同意他的猜想吗?说明你的理由.
答案解析收藏纠错 + 选题
24. (2023七上·从江期中)
1. （1） [观察思考]
  如图(1)所示直线l上有2个点，则图中有条可用图中字母表示的射线，有条线段.
  如图(2)所示直线l上有3个点，则图中有条可用图中字母表示的射线，有条线段.
2. （2） [模型建构]
  如图(3)所示直线l上有n个点，则图中有条可用图中字母表示的射线，有条线段.
3. （3） [拓展应用]
  根据(3)中发现的规律解决问题：某校七年级共有6个班进行足球比赛，准备进行循环赛(即每两队之间赛一场)，预计全部赛完共需多少场比赛?
答案解析收藏纠错 + 选题
25. (2024七上·上城期末) 如图所示，点P是线段AB上任意一点，AB=12 cm，C，D两点分别从点P，B同时向点A运动，且点C的运动速度为2 cm/s，点D的运动速度为3 cm/s，运动时间为t s.
1. （1）若AP=8 cm：
  ①两点运动1 s后，求CD的长；
  ②当点D在线段PB上运动时，试说明：AC=2CD；
2. （2）当t=2时，CD=1 cm，试探索AP的长.
答案解析收藏纠错 + 选题