 B .
B .  C .
C .  D .
D . 
 B .
B . 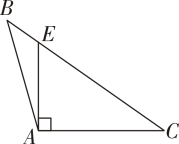 C .
C . 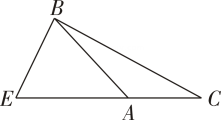 D .
D . 



学习了三角形全等的判定方法(即“SAS”“ASA”“AAS”“SSS”)和直角三角形全等的判定方法(即“HL”)后、我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
【初步思考】
我们不妨将问题用符号语言表示为:在和
中,
,
,
, 然后,对
进行分类,可分为“
是直角、钝角、锐角”三种情况进行探究.
【逐步探究】

已知:如图②,在和
中,
,
, ∠B=∠E,且
,
都是钝角,求证
;
在和
中,
,
,
, 且
,
都是锐角,若
时,则
.