四川省成都市锦江区教科院附中2023-2024学年九年级上学...

更新时间：2024-01-24 浏览次数：34 类型：期中考试

一、选择题（本大题8个小题，每小题4分，共32分，每小题均有4个选项，其中只有一项符合题目要求，答案涂在答题卡上）

1. (2023九上·锦江期中) 一个物体的主视图是三角形，这个物体可能是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2023九上·锦江期中) 用配方法解x²﹣8x+5＝0方程，将其化成（x+a）²＝b的形式，则变形正确的是（　　）

A . （x+4）²＝11 B . （x﹣4）²＝21 C . （x﹣8）²＝11 D . （x﹣4）²＝11

答案解析收藏纠错 + 选题
3. (2023九上·锦江期中) 已知反比例函数y＝ $\text{[math]}$ 的图象经过点（1，6），那么下列四个点中，也在这个函数图象上的是（　　）

A . （﹣2，3） B . （﹣3，2） C . （﹣3，﹣2） D . （6，﹣1）

答案解析收藏纠错 + 选题
4. (2023九上·锦江期中) 在一个不透明的布袋中装有50个黄、白两种颜色的球，除颜色外其他都相同，小红通过多次摸球试验后发现，摸到黄球的频率稳定在0.3左右，则布袋中白球可能有（　　）

A . 40个 B . 35个 C . 20个 D . 15个

答案解析收藏纠错 + 选题
5. (2023九上·锦江期中) 下列说法中，是正方形具有而矩形不具有的性质是（　　）

A . 两组对边分别平行 B . 对角线互相垂直 C . 四个角都为直角 D . 对角线互相平分

答案解析收藏纠错 + 选题
6. (2023九上·锦江期中) 电影《长津湖》上映以来，全国票房连创佳绩．据不完全统计，某市第一天票房约4亿元，以后每天票房按相同的增长率增长，三天后累计票房收入达36亿元，将增长率记作x ，则方程可以列为（　　）

A . 4+4x+4x²＝36 B . 4（1+x）²＝36 C . （1+x）²＝36 D . 4+4（1+x）+4（1+x）²＝36

答案解析收藏纠错 + 选题
7. (2023九上·锦江期中) 如图，在平面直角坐标系xOy中，以点O为位似中心，把△AOB放大到原来的2倍，得到△A'OB'，若点B的对应点B'的坐标是（4，﹣2），则点B的坐标是（　　）

A . （2，1） B . （2，﹣1） C . （﹣2，1） D . （﹣2，﹣1）

答案解析收藏纠错 + 选题
8. (2023九上·锦江期中) 如图，正方形 $\text{[math]}$ 的边 $\text{[math]}$ 在 $\text{[math]}$ 的边 $\text{[math]}$ 上，顶点D、G分别在边 $\text{[math]}$ 上，已知 $\text{[math]}$ 的边 $\text{[math]}$ 长15厘米，高 $\text{[math]}$ 为10厘米，则正方形 $\text{[math]}$ 的边长是（）

A . 4厘米 B . 5厘米 C . 6厘米 D . 8厘米

答案解析收藏纠错 + 选题

二、填空题（本大题共5个小题，每小题4分，共20分，答案写在答题卡上）

9. (2023九上·锦江期中) 若 $\text{[math]}$ ，则 $\text{[math]}$ ＝．

答案解析收藏纠错 + 选题
10. (2023九上·锦江期中) 已知C是线段AB的黄金分割点，AC＞BC ，若AB＝2，则AC的长为．（结果保留根号）

答案解析收藏纠错 + 选题
11. (2023九上·昌邑期中) 反比例函数 $\text{[math]}$ 的图象在第一、三象限，则 $\text{[math]}$ 的取值范围是．

答案解析收藏纠错 + 选题
12. 如图，AB∥CD∥EF ．若 $\text{[math]}$ ， BD＝5，则DF＝．

答案解析收藏纠错 + 选题
13. (2023九上·锦江期中) 如图，正方形ABCD中，M为BC上一点，ME⊥AM ， ME交AD的延长线于点E ，若AB＝8，BM＝6，则DE的长为．

答案解析收藏纠错 + 选题

三、解答题（本大题共5个小题，共48分，答案写在答题卡上）

14. (2023九上·锦江期中)
1. （1）求解下列方程：
  ①x²+2x﹣2＝0；
  ②（2x+3）²＝4（2x+3）．
2. （2）已知关于x的一元二次方程x²+3x+k﹣2＝0有实数根，求k的取值范围．
答案解析收藏纠错 + 选题
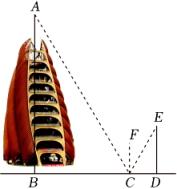
15. (2023九上·锦江期中) 成都熊猫基地瞭望塔可以看到熊猫基地的全貌，还可以看到339电视塔，成为了成都的新地标，也是去成都观光旅游的新景点．小辉想利用所学知识测量瞭望塔的高度（AB），测量方法如下：在地面上点C处平放一面镜子，并在镜子上做一个标记，然后人向后退，直至站在点D处恰好看到瞭望塔AB的顶端A在镜子中的像与镜子上的标记重合，如图，其中B ， C ， D三点在同一直线上．已知小辉的眼睛距离地面的高度ED约为1.75m ，测得BC＝40m ， CD＝1m ，请你帮助他求出该瞭望塔的高度AB ．

答案解析收藏纠错 + 选题
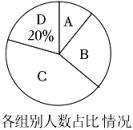
16. (2023九上·锦江期中) 为庆祝中国共产党成立100周年，某中学组织全校学生参加党史知识竞赛，从中任取20名学生的竞赛成绩进行统计，绘制了不完整的统计图表：
组别
成绩范围
频数
A
60～70
2
D
70～80
m
C
80～90
9
D
90～100
n
1. （1）分别求m ， n的值；
2. （2）从A组和D组的学生中随机抽取2名学生，用树状图或列表法求这2名学生都在D组的概率．
答案解析收藏纠错 + 选题
17. (2023九上·锦江期中) 如图，在四边形ABCD中，AB∥DC ， AB＝AD ，对角线AC ， BD交于点O ， AC平分∠BAD ，过点C作CE⊥AB ，交AB的延长线于点E ，连接OE ．
1. （1）求证：四边形ABCD是菱形．
2. （2）若AB＝5，BD＝6，求OE的长．
答案解析收藏纠错 + 选题
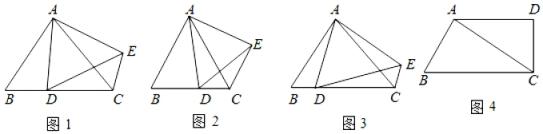
18. (2023九上·锦江期中) 【阅读】如图1，若△ABD∽△ACE ，且点B ， D ， C在同一直线上，则我们把△ABD与△ACE称为旋转相似三角形．
1. （1）【理解】如图2，△ABC和△ADE是等边三角形，点D在边BC上，连接CE ．求证：△ABD与△ACE是旋转相似三角形．
2. （2）【应用】如图3，△ABD与△ACE是旋转相似三角形，AD∥CE ，求证：AC＝DE ．
3. （3）【拓展】如图4，AC是四边形ABCD的对角线，∠D＝90°，∠B＝∠ACD ， BC＝25，AC＝20，AD＝16，试在边BC上确定一点E ，使得四边形AECD是矩形，并说明理由．
答案解析收藏纠错 + 选题

四、填空题（本大题共5个小题，每小题4分，共20分，答案写在答题卡上）

19. (2023九上·锦江期中) 已知代数式a²﹣2a﹣1＝﹣2，那么2a²﹣4a﹣3的值为．

答案解析收藏纠错 + 选题
20. (2024·南京二模) 已知a ， b是方程3x²﹣6x+2＝0的两个根，则a²+b²＝．

答案解析收藏纠错 + 选题
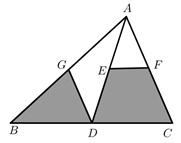
21. (2023九上·锦江期中) 如图， $\text{[math]}$ 是 $\text{[math]}$ 的中线，点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 分别是 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 的中点，连接 $\text{[math]}$ 、 $\text{[math]}$ .现随机向 $\text{[math]}$ 内掷一枚小针，则针尖落在阴影区域的概率是.

答案解析收藏纠错 + 选题
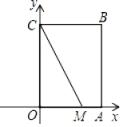
22. (2023九上·锦江期中) 定义：如果一个三角形有一边上的中线等于这条边的一半，那么称三角形为“智慧三角形”．如图，在平面直角坐标系xOy中，矩形OABC的边OA＝3，OC＝4，点M（2，0），在边AB存在点P ，使得△CMP为“智慧三角形”，则点P的坐标为：．

答案解析收藏纠错 + 选题
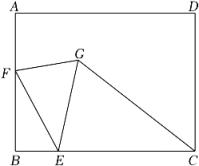
23. (2023九上·锦江期中) 如图，长方形ABCD中，AB＝6，BC＝8，E为BC上一点，且BE＝2，F为AB边上的一个动点，连接EF ，将EF绕着点E顺时针旋转30°到EG的位置，连接FG和CG ，则CG的最小值为．

答案解析收藏纠错 + 选题

五、解答题（本大题共3个小题，共30分，答案写在答题卡上）

24. (2023九上·锦江期中) 顺德华侨城景区在2022年春节长假期间，共接待游客达20万人次，预计在2024年春节长假期间，将接待游客达28.8万人次．
1. （1）求顺德华侨城景区2022至2024年春节长假期间奇游客人次的年平均增长率；
2. （2）华侨城景区一奶茶店销售一款奶茶，每杯成本价为6元，根据销售经验，在旅游旺季，若每杯定价25元，则平均每天可销售300杯，若每杯价格降低1元，则平均每天可多销售30杯.2024年春节期间，店家决定进行降价促销活动，则当每杯售价定为多少元时，既能让顾客获得最大优惠，又可让店家在此款奶茶实现平均每天6300元的利润额？
答案解析收藏纠错 + 选题
25. (2023九上·锦江期中) 如图，在平面直角坐标系xOy中，直线 $\text{[math]}$ 与x轴、y轴分别交于点A、点B ，点D（0，﹣6）在y轴的负半轴上，若将△DAB沿直线AD折叠，点B恰好落在x轴正半轴上的点C处．
1. （1）求直线CD的函数解析式；
2. （2）在直线AB上是否存在一点P ，使得△PBO与△ADC相似？若存在，求点P的坐标；若不存在，请说明理由；
3. （3）现定义：平面内一点到三角形三边所在的直线距离之和等于该三角形周长的一半时，这个点称为此三角形的和谐点．在直线AD上是否存在△COD的和谐点？若存在，请求出和谐点的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题
26. (2023九上·锦江期中) 在矩形ABCD中，点E为AB边上一动点（不与点A ， B重合），连接CE ，过点E作EF⊥CE ．连接AC、AF、CF ， CF与EF分别交AD于点G ， H ．
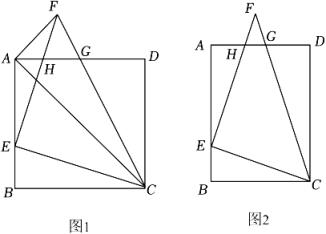
1. （1）如图1，当矩形ABCD为正方形时，且EF＝CE ．求证：△BCE∽△ACF；
2. （2）在（1）的条件下，且点E为AB的中点，求 $\text{[math]}$ 的值；
3. （3）如图2，已知：AB＝8，BC＝6， $\text{[math]}$ ，连接CF交AD于G ， EF与AD交于H ，若FG＝FH ，求BE的长度．
答案解析收藏纠错 + 选题