广东省东莞市重点实验中学2023-2024学年高二上学期数学...

更新时间：2024-01-21 浏览次数：15 类型：月考试卷

一、单选题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1. (2023高二上·东莞月考) 若直线过点(1，2)，(4，2＋ $\text{[math]}$ )，则此直线的倾斜角是（）

A . 30° B . 45° C . 60° D . 90°

答案解析收藏纠错 + 选题
2. (2023高二上·东莞月考) 已知曲线 $\text{[math]}$ ： $\text{[math]}$ ，则其渐近线方程是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023高二上·东莞月考) 已知空间中直线 $\text{[math]}$ 的方向向量为 $\text{[math]}$ ，平面 $\text{[math]}$ 的法向量为 $\text{[math]}$ ，若 $\text{[math]}$ ，则实数 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023高二上·东莞月考) 如图所示，已知某梯子共有5级，从上往下数，第1级的宽为35厘米，第5级的宽为43厘米，且各级的宽度从小到大构成等差数列，则第3级的宽度是（）

A . 39厘米 B . 40厘米 C . 41厘米 D . 42厘米

答案解析收藏纠错 + 选题
5. (2023高二上·东莞月考) 双曲线 $\text{[math]}$ （ $\text{[math]}$ ）的离心率是 $\text{[math]}$ ，则实数 $\text{[math]}$ 的值是（）

A . 12 B . 16 C . 20 D . 24

答案解析收藏纠错 + 选题
6. (2023高二上·东莞月考) 已知数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和 $\text{[math]}$ ，满足条件 $\text{[math]}$ ，则 $\text{[math]}$ 的值是（）

A . 4044 B . 4045 C . 4046 D . 4047

答案解析收藏纠错 + 选题
7. (2023高二上·东莞月考) 已知线段 $\text{[math]}$ 的端点 $\text{[math]}$ 的坐标 $\text{[math]}$ ，端点 $\text{[math]}$ 在圆 $\text{[math]}$ 上运动，求线段 $\text{[math]}$ 的中点 $\text{[math]}$ 的轨迹所围成图形的面积（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023高二上·东莞月考) 在两条异面直线 $\text{[math]}$ ， $\text{[math]}$ 上分别取点 $\text{[math]}$ ， $\text{[math]}$ 和点 $\text{[math]}$ ， $\text{[math]}$ ，使 $\text{[math]}$ ，且 $\text{[math]}$ .已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则两条异面直线 $\text{[math]}$ ， $\text{[math]}$ 所成的角为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、多选题：本题共4小题，每小题5分，共20分.在每小题给出的四个选项中，有多项是符合题目要求的.全部选对的得5分，部分选对的得2分，有选错的得0分.

9. (2023高二上·东莞月考) 已知直线 $\text{[math]}$ ： $\text{[math]}$ ， $\text{[math]}$ ： $\text{[math]}$ （ $\text{[math]}$ ），则（）

A . 直线 $\text{[math]}$ 过定点 $\text{[math]}$ B . 当 $\text{[math]}$ 时， $\text{[math]}$ C . 当 $\text{[math]}$ 时，两直线 $\text{[math]}$ ， $\text{[math]}$ 之间的距离为1 D . 当 $\text{[math]}$ 时， $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023高二上·东莞月考) 圆 $\text{[math]}$ ： $\text{[math]}$ 和圆 $\text{[math]}$ ： $\text{[math]}$ 的公共点为 $\text{[math]}$ ， $\text{[math]}$ ，则有（）

A . 公共弦 $\text{[math]}$ 所在直线方程为 $\text{[math]}$ B . 公共弦 $\text{[math]}$ 的长为 $\text{[math]}$ C . 线段 $\text{[math]}$ 中垂线方程为 $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2023高二上·东莞月考) 已知曲线 $\text{[math]}$ 的方程为 $\text{[math]}$ ，则 $\text{[math]}$ 可能是（）

A . 半径为 $\text{[math]}$ 的圆 B . 焦点在 $\text{[math]}$ 上的椭圆，且长轴长为 $\text{[math]}$ C . 等轴双曲线 D . 焦点在 $\text{[math]}$ 上的双曲线，且焦距为 $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2023高二上·东莞月考) 如图，棱长为1的正方体 $\text{[math]}$ 中， $\text{[math]}$ 为线段 $\text{[math]}$ 上的动点（不含端点），则下列说法中正确的是（）

A . 平面 $\text{[math]}$ 平面 $\text{[math]}$ B . 多面体 $\text{[math]}$ 的体积为定值 C . $\text{[math]}$ 恒为锐角三角形 D . 直线 $\text{[math]}$ 与 $\text{[math]}$ 所成的角可能为 $\text{[math]}$

答案解析收藏纠错 + 选题

三、填空题：本题共4小题，每小题5分，共20分.

13. (2023高二上·东莞月考) 使得“对于任意 $\text{[math]}$ ， $\text{[math]}$ 是递减数列”为真命题的整数 $\text{[math]}$ 值是.（写出一个符合要求的答案即可）

答案解析收藏纠错 + 选题
14. (2023高二上·东莞月考) 如图，在空间平移 $\text{[math]}$ 到 $\text{[math]}$ ，连接对应顶点.设 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 中点，则用基底 $\text{[math]}$ 表示向量 $\text{[math]}$ .

答案解析收藏纠错 + 选题
15. (2023高二上·东莞月考) 数学家欧拉1765在其所著的《三角形几何学》一书中提出：任意三角形的外心、重心、垂心在同一条直线上，后人称这条直线为欧拉线.已知 $\text{[math]}$ 的顶点分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的欧拉线方程是.

答案解析收藏纠错 + 选题
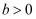
16. (2023高二上·东莞月考) 已知双曲线 $\text{[math]}$ ： $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ ）的左、右焦点分别为 $\text{[math]}$ ， $\text{[math]}$ ，过点 $\text{[math]}$ 作直线交两条渐近线于点 $\text{[math]}$ 、 $\text{[math]}$ ，且 $\text{[math]}$ ，若点 $\text{[math]}$ 在 $\text{[math]}$ 轴上的射影为 $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题

四、解答题：本题共6小题，其中第17题10分，其他题12分，共70分.

17. (2023高二上·东莞月考) 记 $\text{[math]}$ 是等差数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和，若 $\text{[math]}$ .
1. （1）求数列 $\text{[math]}$ 的通项公式 $\text{[math]}$ ；
2. （2）求使 $\text{[math]}$ 成立的 $\text{[math]}$ 的最小值.
答案解析收藏纠错 + 选题
18. (2023高二上·东莞月考) 如图，在直三棱柱 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 的中点， $\text{[math]}$ .
1. （1）求异面直线 $\text{[math]}$ 与 $\text{[math]}$ 夹角的余弦值
2. （2）求点 $\text{[math]}$ 平面 $\text{[math]}$ 的距离.
答案解析收藏纠错 + 选题
19. (2023高二上·东莞月考) 已知抛物线 $\text{[math]}$ ： $\text{[math]}$ （ $\text{[math]}$ ）经过点 $\text{[math]}$ .
1. （1）求抛物线 $\text{[math]}$ 的方程及其焦点坐标、准线方程；
2. （2）过抛物线 $\text{[math]}$ 上一动点 $\text{[math]}$ 作圆 $\text{[math]}$ ： $\text{[math]}$ 的一条切线，切点为 $\text{[math]}$ ，求切线长 $\text{[math]}$ 的最小值.
答案解析收藏纠错 + 选题
20. (2023高二上·东莞月考) 在三棱柱 $\text{[math]}$ 中，侧面正方形 $\text{[math]}$ 的中心为点 $\text{[math]}$ ， $\text{[math]}$ 平面 $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 满足 $\text{[math]}$ （ $\text{[math]}$ ）.
1. （1）求直线 $\text{[math]}$ 与平面 $\text{[math]}$ 的夹角正弦值；
2. （2）若平面 $\text{[math]}$ 与平面 $\text{[math]}$ 的夹角的余弦值为 $\text{[math]}$ ，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
21. (2023高二上·东莞月考) 在我国960万平方千米的大地之下拥有超过35000座，总长接近赤道长度的隧道（约37000千米）.这些隧道样式多种多样，它们或傍山而过，上方构筑顶棚形成“明洞”；或挂于峭壁，每隔一段开出“天窗”形成挂壁公路.但是更多时候它们都隐伏于山体之中，只露出窄窄的出入口洞门.东莞某学生学过圆的知识后受此启发，为山体隧道设计了一个圆弧形洞门样式，如图所示，路宽 $\text{[math]}$ 为16米，洞门最高处距路面4米.
1. （1）建立适当的平面直角坐标系，求圆弧 $\text{[math]}$ 的方程.
2. （2）为使双向行驶的车辆更加安全，该同学进一步优化了设计方案，在路中间建立了2米宽的隔墙.某货车装满货物后整体呈长方体状，宽2米，高3.6米，则此货车能否通过该洞门？并说明理由.
答案解析收藏纠错 + 选题
22. (2023高二上·东莞月考) 已知椭圆 $\text{[math]}$ ： $\text{[math]}$ （ $\text{[math]}$ ）经过三点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 中的两点.
1. （1）求 $\text{[math]}$ 的方程；
2. （2）过 $\text{[math]}$ 的右焦点的直线 $\text{[math]}$ 与 $\text{[math]}$ 交于 $\text{[math]}$ ， $\text{[math]}$ 两点，在直线 $\text{[math]}$ 上是否存在一点 $\text{[math]}$ ，使得 $\text{[math]}$ 是以 $\text{[math]}$ 为斜边的等腰直角三角形？若存在，求出 $\text{[math]}$ 的方程；若不存在，请说明理由.
答案解析收藏纠错 + 选题