 B .
B .  C .
C .  D .
D . 
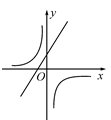 B .
B .  C .
C .  D .
D . 



梅涅劳斯是公元
世纪时的希腊数学家兼天文学家,著有几何学和三角学方面的许多书籍
梅涅劳斯发现,若一条直线与三角形的三边或其延长线相交
交点不能是三角形的顶点
, 可以得到六条线段,三条不连续线段的乘积等于剩下三条线段的乘积
该定理被称为梅涅劳斯定理,简称梅氏定理.

如图 , 直线
交线段
于点
, 交线段
于点
, 交
延长线于点
, 可截得六条线段
、
、
、
、
、
, 则这六条线段满足
.
下面是该定理的一部分证明过程:
证明:如图 , 过点
作
, 交
延长线于点
, 则有
依据
,
【问题情境】
“综合与实践课”上,老师提出:在研究图形的变化时,要多关注运动过程中的不变量,如图 , 四边形
是正方形,点
在边
上运动,连接
, 以
为对角线构造正方形
, 连接
,
.

“善思小组”发现,在点运动的过程中,线段
与
的数量关系保持不变
请直接写出
与
的数量关系: ;
“缜密小组”注意到,当点运动时,
与
的比值也保持不变
请你求出这个比值;
如图 , 连接
, 交
于点
, 若
,
, 请求出
的值.