甘肃省庆阳市西峰区黄官寨实验学校2023-2024学年九年级...

更新时间：2024-04-10 浏览次数：15 类型：期中考试

一、选择题：本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目的要求的．

1. (2023九上·西峰期中) 下列四个图形中属于中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2023九上·西峰期中) 一元二次方程x（x+5）=0的根是（）

A . x₁=0，x₂=5 B . x₁=0，x₂=﹣5 C . x₁=0，x₂= $\text{[math]}$ D . x₁=0，x₂=﹣ $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024九上·珠海期中) 已知方程 $\text{[math]}$ 的两个根是 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . 1 B . $\text{[math]}$ C . 6 D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023九上·西峰期中) 用配方法解方程 $\text{[math]}$ ，经过配方，得到（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023九上·西峰期中) 由二次函数 $\text{[math]}$ 可知（）

A . 其图象的开口向下 B . 其图象的对称轴为 $\text{[math]}$ C . 其最大值为1 D . 当 $\text{[math]}$ 时，y随x的增大而减小

答案解析收藏纠错 + 选题
6. (2023九上·西峰期中) 如图中∠BOD的度数是（）

A . 150^° B . 125° C . 110° D . 55°

答案解析收藏纠错 + 选题
7. (2023九上·西峰期中) 如图，在半径为10的 $\text{[math]}$ 中， $\text{[math]}$ 垂直弦 $\text{[math]}$ 于点 $\text{[math]}$ ，则 $\text{[math]}$ 的长是（）

A . 3 B . 4 C . 6 D . 8

答案解析收藏纠错 + 选题
8. (2023九上·西峰期中) 若 $\text{[math]}$ 为二次函数 $\text{[math]}$ 的图像上的三点，则 $\text{[math]}$ 的大小关系是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2023九上·西峰期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，将 $\text{[math]}$ 在平面内绕点A逆时针旋转到 $\text{[math]}$ 的位置，使 $\text{[math]}$ ，则旋转角的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023九上·西峰期中) 如图，正方形ABCD中，AB=8cm，对角线AC，BD相交于点O，点E，F分别从B，C两点同时出发，以1cm/s的速度沿BC，CD运动，到点C，D时停止运动，设运动时间为t（s），△OEF的面积为s（cm²），则s（cm²）与t（s）的函数关系可用图象表示为（）

A . B . C . D .

答案解析收藏纠错 + 选题

二、填空题：本大题共8小题，每小题3分，共24分，请将答案直接填在答题纸中对应横线上．

11. (2023九上·西峰期中) 点P（2，﹣1）关于原点的对称点坐标为P′（m，1），则m=．

答案解析收藏纠错 + 选题
12. (2023九上·西峰期中) 三角形两边长分别为2和4，第三边是方程 $\text{[math]}$ 的一个解，则这个三角形的周长是．

答案解析收藏纠错 + 选题
13. (2023九上·西峰期中) 把函数 $\text{[math]}$ 的图象先向右平移2个单位，再向下平移3个单位，得到的抛物线是函数的图象.

答案解析收藏纠错 + 选题
14. (2023九上·西峰期中) 如图，在平面直角坐标系xOy中，已知点A（3，4），将OA绕坐标原点O逆时针旋转90°至OA′，则点A′的坐标是．

答案解析收藏纠错 + 选题
15. (2023九上·西峰期中) 关于x的二次函数y=x²﹣kx+k﹣2的图象与y轴的交点在x轴的上方，请写出一个满足条件的二次函数的表达式：．

答案解析收藏纠错 + 选题
16. (2023九上·西峰期中) 如图，抛物线y=ax²+bx+c与x轴的一个交点是A（1，0），对称轴为直线x=﹣1，则一元二次方程ax²+bx+c=0的解是．

答案解析收藏纠错 + 选题
17. (2023九上·西峰期中) 某种植物的主干长出若干数目的支干，每个支干又长出同样数目的小分支，主干、支干、小分支的总数是91．设每个支干长出 $\text{[math]}$ 个小分支，根据题意列方程为．

答案解析收藏纠错 + 选题
18. (2023九上·西峰期中) 如图， $\text{[math]}$ 是圆 $\text{[math]}$ 的一条弦， $\text{[math]}$ 是圆 $\text{[math]}$ 上一动点且 $\text{[math]}$ 分别是 $\text{[math]}$ 的中点，直线 $\text{[math]}$ 与圆 $\text{[math]}$ 交于点 $\text{[math]}$ 、 $\text{[math]}$ ．若圆 $\text{[math]}$ 的半径为2，则 $\text{[math]}$ 的最大值为．

答案解析收藏纠错 + 选题

三、解答题（本大题共8小题，共66分，解答应写出文字说明、演算步骤或推理过程）

19. (2023九上·西峰期中) 解一元二次方程：
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
20. (2023九上·西峰期中) $\text{[math]}$ 在平面直角坐标系中的位置如图所示，其中每个小正方形的边长为1个单位．
1. （1）画出 $\text{[math]}$ 关于原点O的中心对称图形 $\text{[math]}$ ；
2. （2）在（1）的条件下，请分别写出点A、B、C的对应点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 的坐标．
答案解析收藏纠错 + 选题
21. (2023九上·西峰期中) 某农场要建一个面积为 $\text{[math]}$ 长方形的养鸡场，鸡场的一边靠墙(墙长 $\text{[math]}$ )，另外三边用木栏围成，木栏长 $\text{[math]}$ ，求养鸡场的长和宽各是多少？

答案解析收藏纠错 + 选题
22. (2023九上·西峰期中) 已知关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ ．
1. （1）求证：无论 $\text{[math]}$ 取何值，方程总有两个不相等的实数根：
2. （2）若该方程的一个根为1，求 $\text{[math]}$ 的值及另一个根．
答案解析收藏纠错 + 选题
23. (2023九上·西峰期中) 已知 $\text{[math]}$ 的半径为13，弦 $\text{[math]}$ 平行于 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 和 $\text{[math]}$ 之间的距离．

答案解析收藏纠错 + 选题
24. (2023九上·西峰期中) 某商品的进价为每件40元，售价为每件50元，每个月可卖出210件；如果每件商品的售价每上涨1元，则每个月少卖10件（每件售价不能高于65元），设每件商品的售价上涨x元（x为正整数），每个月的销售利润为y元.
1. （1）求y与x的函数关系式并直接写出自变量x的取值范围；
2. （2）每件商品的售价定为多少元时，每个月可获得最大利润？最大的月利润是多少元？
答案解析收藏纠错 + 选题
25. (2023九上·西峰期中) 如图1，在△ABC中，点P为BC边中点，直线a绕顶点A旋转．若B、P在直线a的异侧，BM⊥直线a于点M，CN⊥直线a于点N，连接PM、PN；
1. （1）延长MP交CN于点E（如图2）．
  ①求证：△BPM≌△CPE；
  
  ②求证：PM＝PN；
2. （2）若直线a绕点A旋转到图3的位置时，点B、P在直线a的同侧，其它条件不变．此时PM＝PN还成立吗？若成立，请给予证明；若不成立，请说明理由；
3. （3）若直线a绕点A旋转到与BC边平行的位置时，其它条件不变．请直接判断四边形MBCN的形状及此时PM＝PN还成立吗？（不必说明理由）
答案解析收藏纠错 + 选题
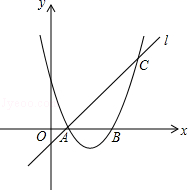
26. (2023九上·西峰期中) 如图，已知抛物线y=ax²+bx+3与x轴交于A、B两点，过点A的直线l与抛物线交于点C，其中A点的坐标是（1，0），C点坐标是（4，3）.
1. （1）求抛物线的解析式；
2. （2）在（1）中抛物线的对称轴上是否存在点D，使△BCD的周长最小？若存在，求出点D的坐标，若不存在，请说明理由；
3. （3）若点E是（1）中抛物线上的一个动点，且位于直线AC的下方，试求△ACE的最大面积及E点的坐标.
答案解析收藏纠错 + 选题