重庆市2024届高三上学期数学第二次质量检测试卷

更新时间：2024-03-07 浏览次数：13 类型：月考试卷

一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项符合题目要求.

1. (2024高三上·重庆月考) 已知全集 $\text{[math]}$ ，集合 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024高三上·重庆月考) 已知 $\text{[math]}$ 是第三象限角，则点 $\text{[math]}$ 位于（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
3. (2024高三上·重庆月考) “ $\text{[math]}$ ”是“幂函数 $\text{[math]}$ 在 $\text{[math]}$ 上单调递增”的（）

A . 充分不必要条件 B . 必要不充分条件 C . 充要条件 D . 既不充分也不必要条件

答案解析收藏纠错 + 选题
4. (2024高三上·重庆月考) 一组数据按从小到大的顺序排列为2，4， $\text{[math]}$ ， 13，16，17，若该组数据的中位数是极差的 $\text{[math]}$ ，则该组数据的40百分位数是（）

A . 4 B . 4.5 C . 5 D . 9

答案解析收藏纠错 + 选题
5. (2024高三上·重庆月考) 已知 $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . -3 B . -1 C . 1 D . 3

答案解析收藏纠错 + 选题
6. (2024高三上·重庆月考) 数列 $\text{[math]}$ 、 $\text{[math]}$ 满足： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则数列 $\text{[math]}$ 的最大项是（）

A . 第7项 B . 第9项 C . 第11项 D . 第12项

答案解析收藏纠错 + 选题
7. (2024高三上·重庆月考) 已知 $\text{[math]}$ ，将 $\text{[math]}$ 向左平移 $\text{[math]}$ 个单位长度，再将横坐标缩短为原来的 $\text{[math]}$ ，得到函数 $\text{[math]}$ .若对 $\text{[math]}$ ，都有 $\text{[math]}$ 成立，则实数 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
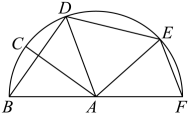
8. (2024高三上·重庆月考) 如图所示，某市拟将一个半圆形的空地改造为果园.设 $\text{[math]}$ ，且 $\text{[math]}$ .若要在扇形 $\text{[math]}$ 和四边形 $\text{[math]}$ 内种满苹果，则当苹果的种植总面积最大时， $\text{[math]}$ 的大小为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、多项选择题：本题共4小题，每小题5分，共20分.在每小题给出的四个选项中，有多项符合题目要求.全部选对得5分，部分选对得2分，有选错得0分.

9. (2024高三上·重庆月考) 已知实数 $\text{[math]}$ ，则下列不等式中一定正确的有（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024高三上·重庆月考) 已知函数 $\text{[math]}$ ，则下列说法中正确的有（）

A . $\text{[math]}$ 是 $\text{[math]}$ 的一个周期 B . $\text{[math]}$ 是 $\text{[math]}$ 的一个对称中心 C . $\text{[math]}$ 在 $\text{[math]}$ 上单调递增 D . 若 $\text{[math]}$ ，则 $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2024高三上·重庆月考) 已知函数 $\text{[math]}$ （ $\text{[math]}$ 且 $\text{[math]}$ ），下列说法正确的有（）

A . 当 $\text{[math]}$ 时， $\text{[math]}$ B . 当 $\text{[math]}$ 时，有 $\text{[math]}$ 恒成立 C . 当 $\text{[math]}$ 时， $\text{[math]}$ 有两个零点 D . 存在唯一的 $\text{[math]}$ 使得 $\text{[math]}$ 仅有一个零点

答案解析收藏纠错 + 选题
12. (2024高三上·重庆月考) 已知双曲线 $\text{[math]}$ ： $\text{[math]}$ 的左、右焦点分别为 $\text{[math]}$ ， $\text{[math]}$ ，过 $\text{[math]}$ 作直线 $\text{[math]}$ 的垂线，垂足为 $\text{[math]}$ ，且与 $\text{[math]}$ 的右支交于点 $\text{[math]}$ ， $\text{[math]}$ 为坐标原点，且 $\text{[math]}$ ，则（）

A . $\text{[math]}$ B . $\text{[math]}$ 的离心率为 $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

三、填空题：本题共4小题，每小题5分，共20分.

13. (2024高三上·重庆月考) $\text{[math]}$ 展开式中的常数项为．

答案解析收藏纠错 + 选题
14. (2024高三上·重庆月考) 若 $\text{[math]}$ ，则 $\text{[math]}$ =.

答案解析收藏纠错 + 选题
15. (2024高三上·重庆月考) 已知 $\text{[math]}$ ， $\text{[math]}$ ，若对 $\text{[math]}$ ， $\text{[math]}$ 使 $\text{[math]}$ 成立，则实数 $\text{[math]}$ 的取值范围是.

答案解析收藏纠错 + 选题
16. (2024高三上·重庆月考) 已知函数 $\text{[math]}$ .如图，直线 $\text{[math]}$ 与曲线 $\text{[math]}$ 交于 $\text{[math]}$ ， $\text{[math]}$ 两点， $\text{[math]}$ ，则 $\text{[math]}$ =. $\text{[math]}$ 在区间 $\text{[math]}$ 上的最大值与最小值的差的范围是.

答案解析收藏纠错 + 选题

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

17. (2024高三上·重庆月考) 记数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和为 $\text{[math]}$ ，且 $\text{[math]}$ .
1. （1）求证：数列 $\text{[math]}$ 是等比数列；
2. （2）求证： $\text{[math]}$ .
答案解析收藏纠错 + 选题
18. (2024高三上·重庆月考) 在四棱锥 $\text{[math]}$ 中，平面 $\text{[math]}$ 平面 $\text{[math]}$ ，侧面 $\text{[math]}$ 是等边三角形， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 在棱 $\text{[math]}$ 上，且满足 $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ ；
2. （2）求二面角 $\text{[math]}$ 的余弦值.
答案解析收藏纠错 + 选题
19. (2024高三上·重庆月考) 2023年7月28日至8月8日在成都举行的第三十一届世界大学生夏季运动会是中国西部第一次举办世界性综合运动会.在本届成都大运会中，共有800多支城市志愿服务队139万青年志愿者参加.现某城市志愿服务队通过报名者对某比赛项目的了解程度进行筛选，筛选规则：对报名者进行分组，每两人一组，同组两人以抢答形式进行比赛，共7道题，抢到并回答正确得一分，答错则对方得一分，先得4分者获胜，比赛结束.已知在这次分组中，甲乙两人被分为一组，已知甲，乙两人都参与每一次抢题，且每次抢到的概率相同，甲和乙正确回答每道题的概率分别是 $\text{[math]}$ 、 $\text{[math]}$ ，且两人各道题是否回答正确均相互独立.
1. （1）在第二道题结束时，求甲：乙的比分为2：0的概率；
2. （2）若已知在第三道题结束时甲得分以2：1领先，设到比赛结束时，两人共再继续抢答了 $\text{[math]}$ 道题，求 $\text{[math]}$ 的分布列和数学期望.
答案解析收藏纠错 + 选题
20. (2024高三上·重庆月考) 在 $\text{[math]}$ 中，角 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的对边分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，已知 $\text{[math]}$ .
1. （1）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的面积；
2. （2）求 $\text{[math]}$ 的最小值，并求出此时 $\text{[math]}$ 的大小.
答案解析收藏纠错 + 选题
21. (2024高三上·重庆月考) 过点 $\text{[math]}$ 作斜率为 $\text{[math]}$ 的直线 $\text{[math]}$ 与抛物线 $\text{[math]}$ ： $\text{[math]}$ 交于 $\text{[math]}$ ， $\text{[math]}$ 两点， $\text{[math]}$ 为坐标原点，当 $\text{[math]}$ 时， $\text{[math]}$ .
1. （1）求抛物线 $\text{[math]}$ 的方程；
2. （2）过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，记 $\text{[math]}$ ， $\text{[math]}$ 面积分别为 $\text{[math]}$ ， $\text{[math]}$ ，求当 $\text{[math]}$ 取得最小值时直线 $\text{[math]}$ 的方程.
答案解析收藏纠错 + 选题
22. (2024高三上·重庆月考) 设函数 $\text{[math]}$ .
1. （1）当 $\text{[math]}$ ， $\text{[math]}$ 时，
  ①求 $\text{[math]}$ 在 $\text{[math]}$ 处的切线方程；
  ②求证：当 $\text{[math]}$ 时， $\text{[math]}$ ；
2. （2）当 $\text{[math]}$ 时，已知 $\text{[math]}$ 为函数 $\text{[math]}$ 的两个零点（ $\text{[math]}$ 为 $\text{[math]}$ 的导数），求证： $\text{[math]}$ .
答案解析收藏纠错 + 选题