吉林省松原市宁江区2023-2024学年九年级上学期数学期末...

更新时间：2024-03-31 浏览次数：19 类型：期末考试

一、单项选择题（每小题2分，共12分）

1. (2024九上·宁江期末) 下列图形分别是可回收物、厨余垃圾、有害垃圾及其它垃圾的标志，其中，既是中心对称图形又是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2024九上·伊通期末) 用配方法解方程 $\text{[math]}$ 时，原方程应变形为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024九上·宁江期末) 下列事件中属于随机事件的是（）

A . 今天是星期一，明天是星期二 B . 从一个装满红球的袋子里摸出了一个白球 C . 掷一枚质地均匀的硬币正面朝上 D . 抛出的篮球会下落

答案解析收藏纠错 + 选题
4. (2024九上·宁江期末) 若A（ $\text{[math]}$ ， $\text{[math]}$ ），B（ $\text{[math]}$ ， $\text{[math]}$ ），C（ $\text{[math]}$ ， $\text{[math]}$ ）为二次函数 $\text{[math]}$ 的图象上的三点，则 $\text{[math]}$ 的大小关系是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024九上·宁江期末) 如图，点P是反比例函数 $\text{[math]}$ 的图象上任意一点，过点P作 $\text{[math]}$ 轴，垂足为M ，若 $\text{[math]}$ 的面积等于3，则k的值等于（　　）

A . $\text{[math]}$ B . 6 C . $\text{[math]}$ D . 3

答案解析收藏纠错 + 选题
6. (2024九上·宁江期末) 如图，AB是⊙O的直径，点C，D，E在⊙O上，若∠AED＝20°，则∠BCD的度数为(　　)

A . 100° B . 110° C . 115° D . 120°

答案解析收藏纠错 + 选题

二、填空题（每小题3分，共24分）

7. (2024九上·宁江期末) 已知 $\text{[math]}$ 是方程 $\text{[math]}$ 的一个根，则方程的另一个根是．

答案解析收藏纠错 + 选题
8. (2024九上·宁江期末) 关于“圆的定义”，在我国古代就有记载，战国时期数学家墨子撰写的《墨经》一书中，就有“圆，一中同长也”的记载，这句话里的“中”字的意思可以理解为．

答案解析收藏纠错 + 选题
9. (2024·市北区模拟) 如图，假设可以随意在图中取点，那么这个点取在阴影部分的概率是．

答案解析收藏纠错 + 选题
10. (2024九上·宁江期末) 如图，学校将一面积为110m²的矩形空地一边增加4m，另一边增加5m后，建成了一个正方形训练场，则此训练场的面积为m² ．

答案解析收藏纠错 + 选题
11. (2024九上·宁江期末) 如图，将 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转 $\text{[math]}$ ，得到 $\text{[math]}$ ，若点 $\text{[math]}$ 恰好在 $\text{[math]}$ 的延长线上，则 $\text{[math]}$ 的度数为．

答案解析收藏纠错 + 选题
12. (2024九下·广州月考) 如图，圆锥的底面半径为1 cm，母线AB的长为3 cm，则这个圆锥侧面展开图扇形的圆心角为度．

答案解析收藏纠错 + 选题
13. (2024九上·宁江期末) 如图，直线 $\text{[math]}$ 与双曲线 $\text{[math]}$ 交于 $\text{[math]}$ 两点，若 $\text{[math]}$ 的面积为4，则k的值为．

答案解析收藏纠错 + 选题
14. (2024九上·宁江期末) 在平面直角坐标系中，抛物线y=ax²+bx+c（a ， b ， c是常数，a＞0）的部分图象如图所示，直线x=1是它的对称轴．若一元二次方程ax²+bx+c=0的一个根x₁的取值范围是2＜x₁＜3，则它的另一个根x₂的取值范围是．

答案解析收藏纠错 + 选题

三、解答题（每小题5分，共20分）

15. (2024九上·宁江期末) 解方程： $\text{[math]}$

答案解析收藏纠错 + 选题
16. (2024九上·宁江期末) 小晗家客厅里装有一种三位单极开关，分别控制着A（楼梯）、B（客厅）、C（走廊）三盏电灯，在正常情况下，小晗按下任意一个开关均可打开对应的一盏电灯，既可三盏、两盏齐开，也可分别单盏开．因刚搬进新房不久，不熟悉情况．
1. （1）若小晗任意按下一个开关，正好楼梯灯亮的概率是多少？
2. （2）若任意按下其中的两个开关，则正好客厅灯和走廊灯同时亮的概率是多少？请用树状图或列表加以说明．
答案解析收藏纠错 + 选题
17. (2024九上·宁江期末) 抛物线y＝ax²＋bx＋c过(－3，0)，(1，0)两点，与y轴的交点为(0，4)，求抛物线的解析式．

答案解析收藏纠错 + 选题
18. (2024九上·宁江期末) 已知：如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，以 $\text{[math]}$ 为边向形外作等边三角形 $\text{[math]}$ ，把 $\text{[math]}$ 绕着点D按顺时针方向旋转 $\text{[math]}$ 后得到 $\text{[math]}$ ，且A、C、E三点共线，若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的度数与 $\text{[math]}$ 的长．

答案解析收藏纠错 + 选题

四、解答题（每小题7分，共28分）

19. (2024九上·宁江期末) 如图，方格纸中的每个小方格是边长为1个单位的正方形．
1. （1）画出 $\text{[math]}$ 向右平移5个单位长度后的 $\text{[math]}$ ；
2. （2）再将 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ ，画出旋转后的 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
20. (2024九上·乾安期末) 下面是小元设计的“过圆上一点作圆的切线”的尺规作图过程．
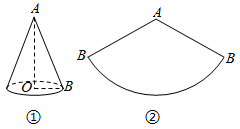
已知：如图，⊙O及⊙O上一点P．
求作：过点P的⊙O的切线．
作法：如图，作射线OP；
① 在直线OP外任取一点A，以A为圆心，AP为半径作⊙A，与射线OP交于另一点B；
②连接并延长BA与⊙A交于点C；
③作直线PC；
则直线PC即为所求．根据小元设计的尺规作图过程，
1. （1）使用直尺和圆规，补全图形；（保留作图痕迹）
2. （2）完成下面的证明：
  证明：∵ BC是⊙A的直径，
  ∴ ∠BPC=90°（）（填推理依据）．
  ∴ OP⊥PC．
  又∵ OP是⊙O的半径，
  ∴ PC是⊙O的切线（）（填推理依据）．
答案解析收藏纠错 + 选题
21. (2024九上·宁江期末) 关于x的一元二次方程x²﹣x﹣（m+1）=0有两个不相等的实数根.
1. （1）求m的取值范围；
2. （2）若m为符合条件的最小整数，求此方程的根.
答案解析收藏纠错 + 选题
22. (2024九上·宁江期末) 已知抛物线 $\text{[math]}$ 与y轴交于点A，点A与点B关于抛物线的对称轴对称.直线 $\text{[math]}$ 经过点B且与 $\text{[math]}$ 轴垂直.
1. （1）求抛物线的顶点C的坐标和直线 $\text{[math]}$ 的表达式.
2. （2）抛物线与直线 $\text{[math]}$ 交于点P，当OP≤5时，求 $\text{[math]}$ 的取值范围.
答案解析收藏纠错 + 选题

五、解答题（每小题8分，共16分）

23. (2024九上·宁江期末) 如图 $\text{[math]}$ 的图像交x轴于点 $\text{[math]}$ ，交反比例函数 $\text{[math]}$ 的图像于点B（1，m）．
1. （1）求反比例函数的表达式；
2. （2）点D为反比例函数图象第一象限上B点下方一个动点，过点D作 $\text{[math]}$ 轴交线段AB于点C ，连接AD ，求 $\text{[math]}$ 的面积的最大值．
答案解析收藏纠错 + 选题
24. (2024九上·宁江期末) 扬州市为打造“绿色城市”降低空气中pm₂_.5的浓度，积极投入资金进行园林绿化工程，已知2014年投资1000万元，预计2016年投资1210万元．若这两年内平均每年投资增长的百分率相同．
1. （1）求平均每年投资增长的百分率；
2. （2）经过评估，空气中pm₂_.5的浓度连续两年较上年下降10%，则两年后pm₂_.5的浓度比最初下降了百分之几？
答案解析收藏纠错 + 选题

六、解答题（每小题10分，共20分）

25. (2024九上·宁江期末)
1. （1）【性质探究】如图1，在 $\text{[math]}$ 中， $\text{[math]}$ ， AB＝AC ，点D在斜边BC上，将△ABD绕点A逆时针旋转90°得到△ACE．
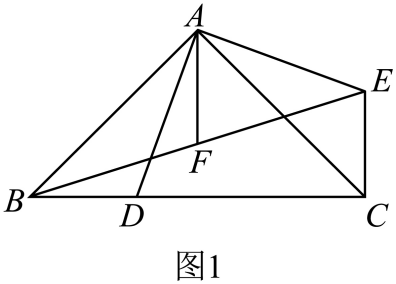
  ①直线BD与CE的位置关系为；
  ②若点F为BE的中点，连接AF ，请探究线段AF与CD的数量关系，并给予证明．
2. （2）【拓展应用】
  如图2，已知点E是正方形ABCD的边BC上任意一点，以AE为边作正方形AEFG ，连接BG，点H为BG的中点，连接AH ．若AB＝4，BE＝3，求AH的长．
答案解析收藏纠错 + 选题
26. (2024九上·宁江期末) 【生活情境】
为美化校园环境，某学校根据地形情况，要对景观带中一个长 $\text{[math]}$ ，宽 $\text{[math]}$ 的长方形水池 $\text{[math]}$ 进行加长改造（如图①，改造后的水池 $\text{[math]}$ 仍为长方形，以下简称水池1），同时，再建造一个周长为 $\text{[math]}$ 的矩形水池 $\text{[math]}$ （如图②，以下简称水池2）．
【建立模型】
如果设水池 $\text{[math]}$ 的边 $\text{[math]}$ 加长长度 $\text{[math]}$ 为 $\text{[math]}$ ，加长后水池1的总面积为 $\text{[math]}$ ，则 $\text{[math]}$ 关于 $\text{[math]}$ 的函数解析式为： $\text{[math]}$ ；设水池2的边 $\text{[math]}$ 的长为 $\text{[math]}$ ，面积为 $\text{[math]}$ ，则 $\text{[math]}$ 关于 $\text{[math]}$ 的函数解析式为： $\text{[math]}$ ，上述两个函数在同一平面直角坐标系中的图像如图③．
【问题解决】
1. （1）若水池2的面积随 $\text{[math]}$ 长度的增加而减小，则 $\text{[math]}$ 长度的取值范围是（可省略单位），水池2面积的最大值是 $\text{[math]}$ ；
2. （2）在图③字母标注的点中，表示两个水池面积相等的点是，此时的 $\text{[math]}$ 值是；
3. （3）当水池1的面积大于水池2的面积时， $\text{[math]}$ 的取值范围是；
4. （4）在 $\text{[math]}$ 范围内，求两个水池面积差的最大值和此时 $\text{[math]}$ 的值；
5. （5）假设水池 $\text{[math]}$ 的边 $\text{[math]}$ 的长度为 $\text{[math]}$ ，其他条件不变（这个加长改造后的新水池简称水池3），则水池3的总面积 $\text{[math]}$ 关于 $\text{[math]}$ 的函数解析式为： $\text{[math]}$ ．若水池3与水池2的面积相等时， $\text{[math]}$ 有唯一值，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题